Bayesian Modelling by Zoubin Ghahramani, MLSS2012, Univ of Cambridge
2012 영국 케임브리지 대학교 여름방학 머신러닝 강의 요약
베이지안 머신러닝에 대해 인터넷에서 자료를 찾다보니 꽤 괜찮은 동영상 강의가 있어서 요약해보았다. 베이지안 모델링에 대해 개괄적으로 설명해주는 강의인데, 머신러닝에서 베이즈 정리가 어떻게 쓰이는지 잘 설명된 자료인 것 같다.
http://videolectures.net/mlss2012_ghahramani_bayesian_modelling/
위 링크에서 해당 강의 자료를 다운받고 시청할 수 있다. 다만 어도비 플래시가 있어야 구동이 되니 아마 올해가 지나면 못 듣지 않을까 싶다. 베이지안 모델링 외에도 Bayesian Nonparametrics, Graphical Model 등등 다른 다양한 강의가 있으니 한번 참고해보자.
아래에다가 강의 슬라이드별로 강의에서 아저씨가 말씀하신 부분을 나름 보충을 섞어 요약해놨다. 그래도 강의를 직접 보는 편이 도움이 많이 될 것.
강의 내용 요약



- 데이터에 대한 모델이 만족해야될 요건은, 일단 데이터에 내재한 불확실성을 잘 반영해야 함. 그 불확실성은 1) 데이터 자체의 노이즈와, 2) 진짜 모델과 모수에 대해 잘 모르기 때문에 발생함.
- 데이터의 크기와 변동에 대해서 Robust 해야 한다.

- 모델이란 “a description of possible data one could observe from a system” 즉 실제 데이터 형성 과정에 대한 설명이 바로 모델이다.
- 실제 데이터 형성 과정을 잘 반영한다는 것은 예측 결과가 실제와 잘 맞아야한다는 것이다.
- 미적분이 “rate of change"에 대해 설명하는 수학적 언어였다면 확률은 “uncertainty"에 대해 이야기하는 수학적 언어이다. 때문에 자연스럽게 데이터에 내재된 불확실성을 잘 반영하기 위해서는 확률 모델을 쓰는 것이다.
- 확률 모델을 쓰기 때문에 우리는 베이즈 정리를 사용해 데이터에서 관측되지 않는 미지의 양에 대한 추론을 하고, 새로운 관측치에 대한 예측도 하고, 데이터에서 배울 수 있는 것.

- 베이즈 정리가 대단한 이유는
- 데이터를 보기 전에 대한 가설에 대한 믿음과
- 데이터를 보고 난 후의 가설에 대한 믿음을 매끄럽게 연결해주기 때문
- 이 연결고리가 바로 Likelihood이다. Likelihood의 역할은 어떤 가설에 대하여 데이터에 확률을 부여하는 것.
- 때문에 가설이 “well formulated"되기 위한 요건은 바로 데이터에 확률을 부여할 수 있어야 한다.
- 긍까 존나 자세해야 된다는 거임. 그냥 y와 x의 관계는 선형이다! 하면 안 되고 베타는 -1부터 1까지의 유니폼 분포를 따르고, 오차항은 가우시안이고, 등등 가정을 계속 써나가다 보면 어떤 순간 Likelihood가 탄생한다.
- 즉 Likelihood는 데이터에 대한 가정이, 데이터에 대해 확률을 부여할 수 있을 정도로 자세하게 정의된 것.
- 베이지안 모델러들은 Likelihood와 Prior를 같이 먼저 정해야한다. 이게 바로 베이지안 모델임.

- 머신러닝의 목적을 크게 두 가지 보자면
- 데이터의 형성 과정, 즉 모델을 배우기 위해 머신러닝 알고리즘을 사용
- 일단 데이터 다운 받고 모든 알고리즘을 다 돌려본 다음에 가장 잘 나온 거 가지고 예측하고 결정하고… 그냥 다 때려넣어보는 것. 굳이 모델을 찾겠다는 마인드가 아님

- 목차..

- 자세한 목차… 많이 스킵할거임

- 머신러닝의 대표적인 예시를 가지고 설명해보자. 머신러닝에서 확률적인 접근이란 데이터의 형성 과정에 대한 Likelihood 함수를 세우는 것을 의미한다.

- Classification 문제에서 데이터 $x$가 주어졌을 때 $y$가 $-1$ 또는 $1$일 확률을 Likelihood 함수로 나타낼 수 있다.
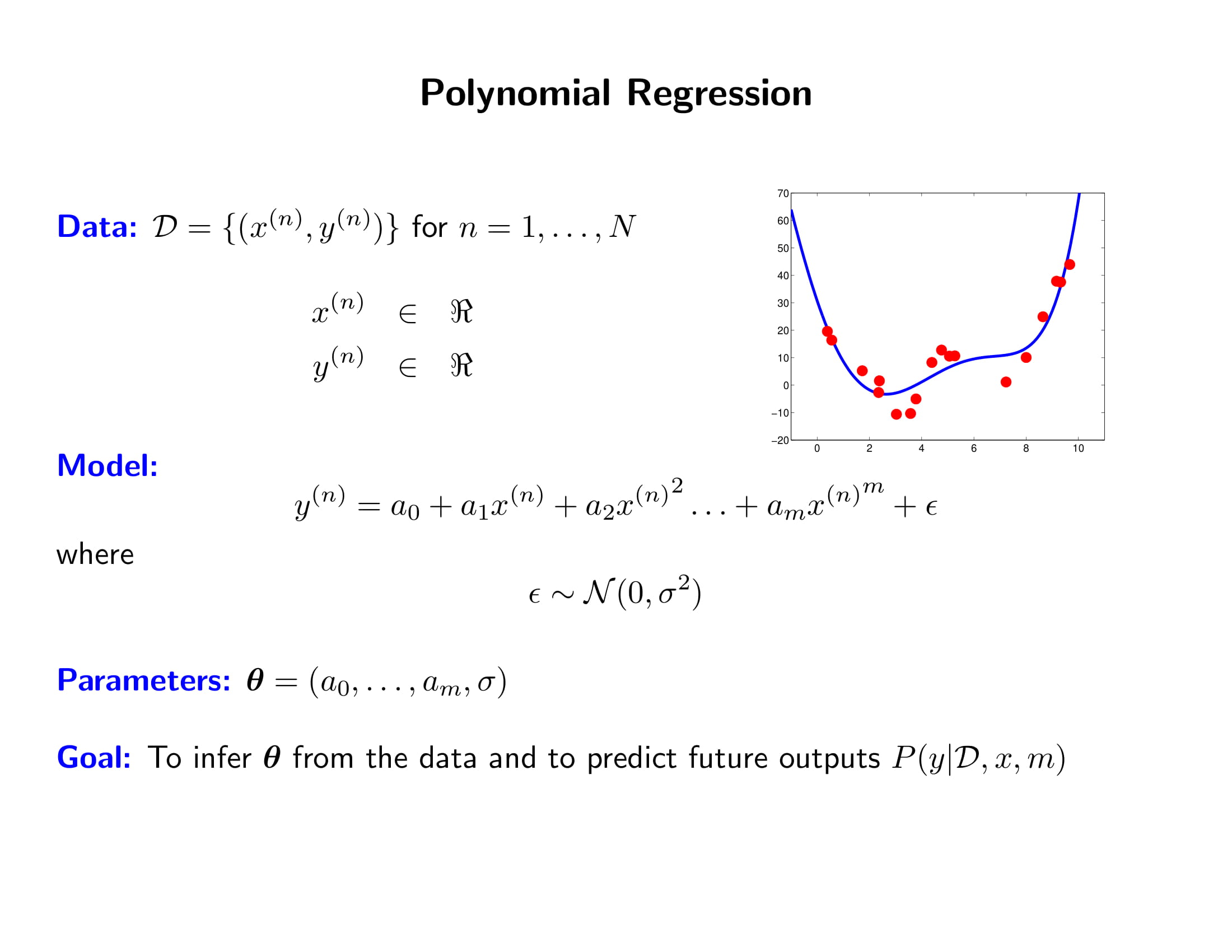
-
고차항 회귀분석에서 오차항의 정규분포를 가정하면 likelihood 함수를 쓸 수 있다. 여기에서 모수에 대해 Prior 믿음을 주고 베이즈 정리로 업데이트를 하면 그것이 Bayesian Linear Regression이 되는 것이다.
-
Bayesian Linear Regression이 잘 설명된 그림이 아래 그림이다. (출처)
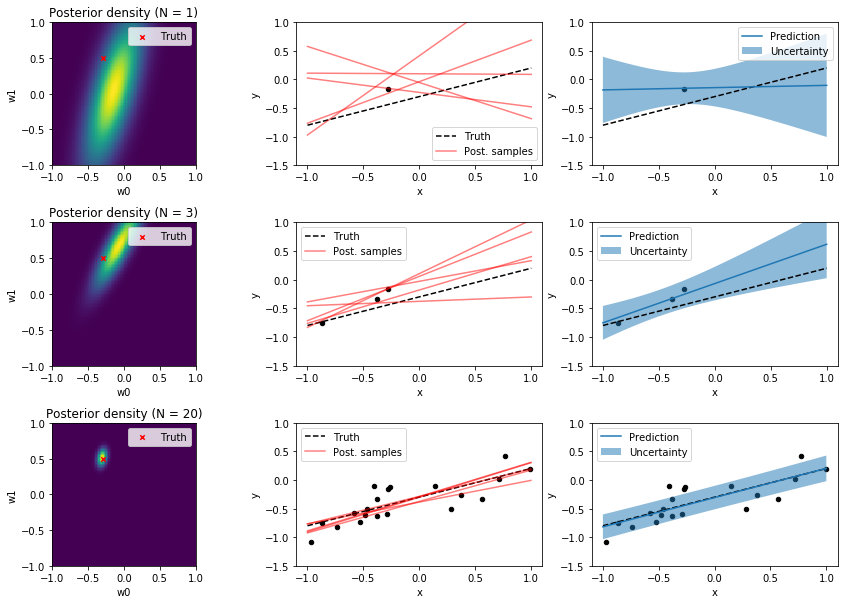
맨 왼쪽 열이 parameter space에 그려진 모수에 대한 믿음의 분포이며, 이 분포에서 추출한 모수(회귀선)이 그려진 것이 가운데 그림이고, 이에 대응하는 posterior predictive 분포가 제일 오른쪽에 있는 열이다.

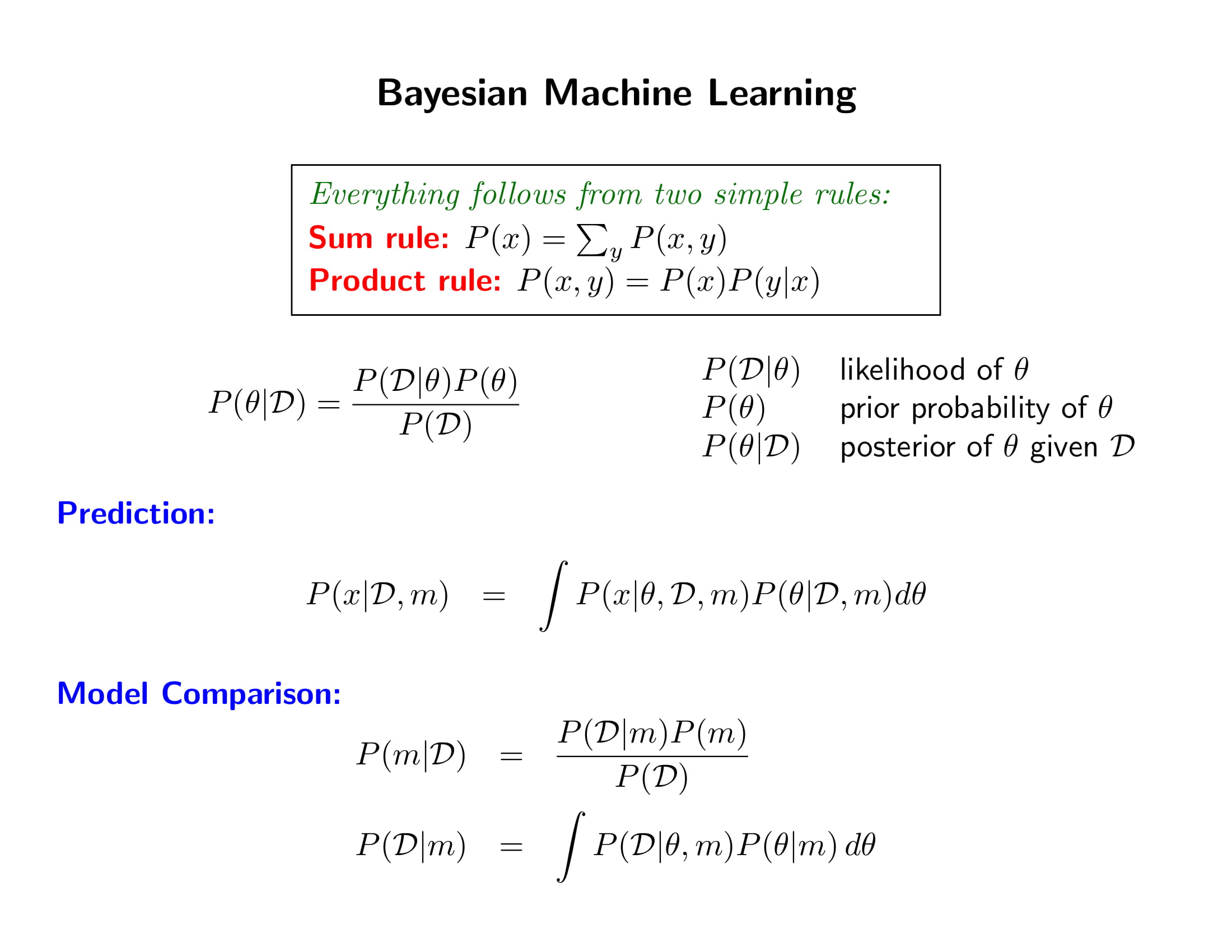
- Likelihood 나왔지? 베이즈 룰 써라. 끝.
- 솔직히 베이즈 룰이라고 거창하게 말할 것도 없이 그냥 Sum rule하고 Product rule만 알면 끝이다.
- prediction? average 때려라!

- 는 훼이크!

- 왜 베이지안이냐? 아니.. 뭐 미적분 쓰면 다 미적부니안인가.. 야 그냥 확률모델 세우니까 당연히 썸룰이랑 프로덕트 룰 쓰는거임… 굳이 베이지안이라고 부르는게 이상함;;

- 정말 당연하다는 거를 느껴보자. 니가 로봇 만든다고 하자. 알고리즘 짤 때 저런거 다 고려해야함. 그럼 베이즈 룰 써야지. ㅇㅋ?
- 즉 여러 가설에 대한 믿음을 수치적으로 나타내려면 확률을 쓰는 거고, 데이터를 보기 전과 본 후의 확률의 변화를 계산하려면 베이즈 룰을 쓸 수 밖에 없다는 것.

- 믿음이 왜 확률이 되는지 자세한 논의. Robot’s belief이 저런 조건들을 다 만족하면 그 belief가 결국 확률의 3공리를 만족해야 한다는 거임. 그래서 베이즈 룰 가능
- 반대로 말하면 확률론이란 합리적인 의사결정주체(rational agent)의 믿음 체계를 나타내는 언어라는 것. “It extends logic to strength of belief”

- Model of economic rationality: economic case for the use of probability to represent belief
- 믿음이 0.9이면 나는 9to1 odd 혹은 그보다 더 좋은 조건을 받아들일 준비가 됐다는 거임
- 뭔 소리임? 그냥 이전의 슬라이드 내용을 다른 방식으로 보인 거임

- Theoretical aspect of bayesian methods
- Bayesian이 꼭 모수를 랜덤변수라고 보는 건 아님. 참 모수의 존재를 인정해도 전혀 문제 없음.
- (어떤 정규성 가정을 만족하면) a priori하게 참 모수 근처에 어떤 확률 mass라도 있으면 데이터가 무한으로 갈수록 우리의 사후믿음은 참모수만 1인 디락 델타 펑션이 수렴할거임
- 우리 prior에 없는 모델이 진짜 답이라도 결국 포스테리어는 실제와 가장 잘 근사한 놈을 집어냄
- MLE와의 차이점은 MLE는 추정량이라는 하나의 값이 참 모수로 확률수렴하다고 얘기한 거라면, 이 정리는 Posterior라는 확률분포 자체가 하나의 분포로 분포수렴한다고 얘기하는 것이다.

- 똑같은 곳으로 수렴하니 둘의 차이는 어심토틸하게 0이 된다.
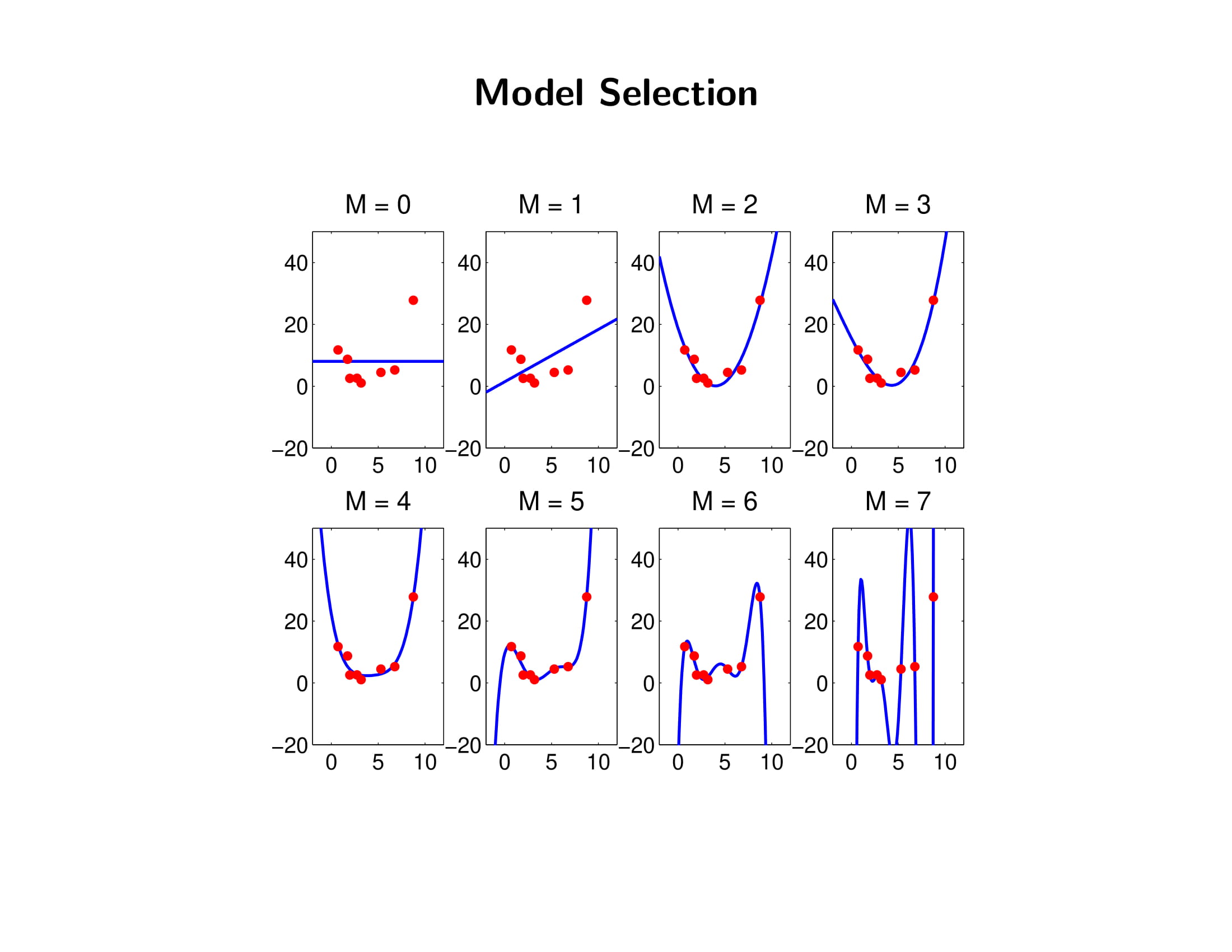
- underfitting과 overfitting을 피하기 위한 베이지안 모델 설렉션을 알아보자.
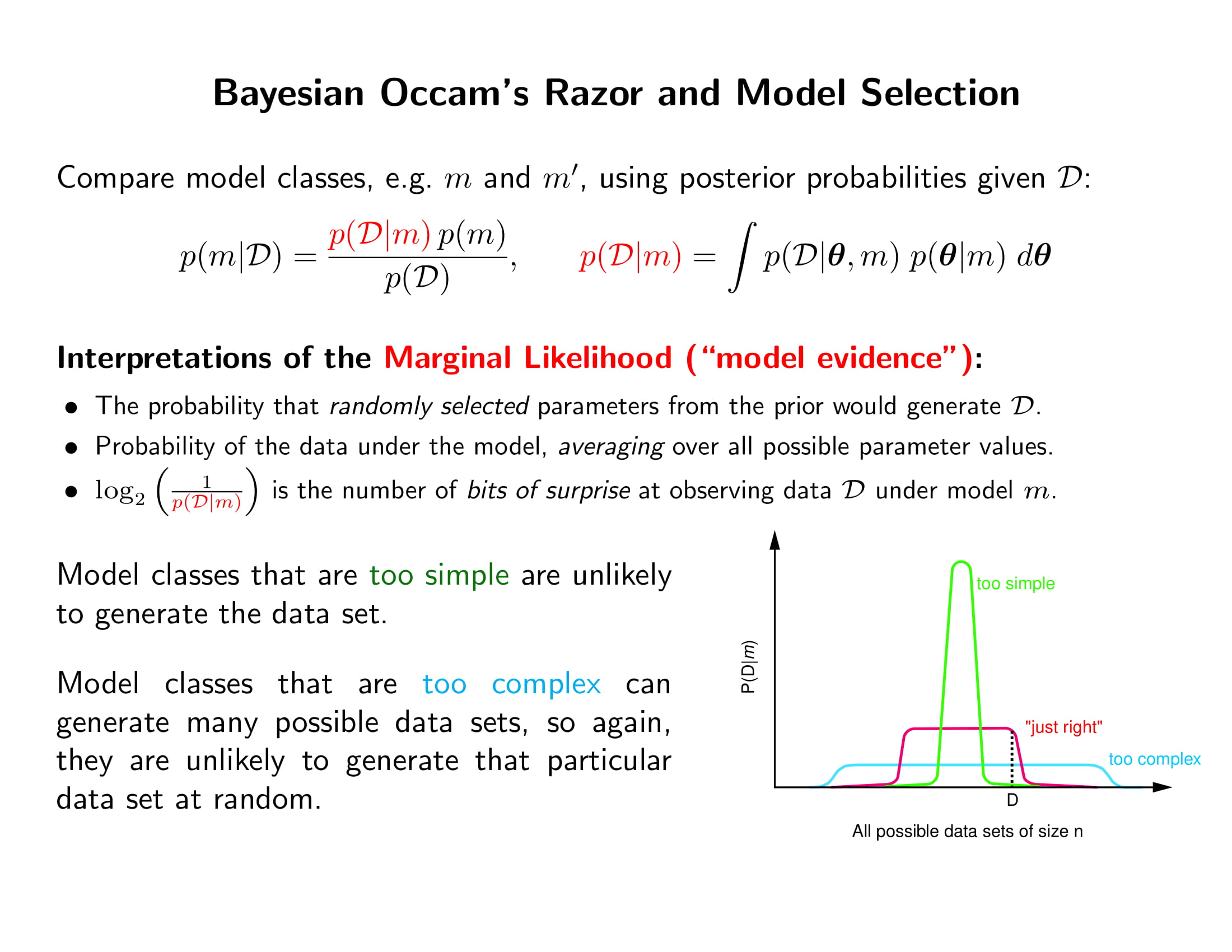
- 데이터 $\mathcal{D}$가 주어진 상태에서 Model evidence $p(\mathcal{D}\mid m)$를 어떻게 계산할 것인가? analytic하게 계산할 수 있으면 제일 좋지. 근데 그게 안 되면…
- 일단 prior $p(\boldsymbol{\theta}\mid m)$에서 $\boldsymbol{\theta}_1$를 랜덤 샘플한 후에 $p(\mathcal{D}\mid \boldsymbol{\theta}_1, m)$를 계산하고, 그걸 한 10000번 해서 $(s=1:10000)$ $p(\mathcal{D}\mid \boldsymbol{\theta}_s, m)$의 평균을 구한다. (몬테카를로 적분)
- 그러나 데이터가 많아질수록 $p(\mathcal{D}\mid \boldsymbol{\theta}, m)$가 아주 그냥 지수적으로 뾰족해지기때문에 needle in a haystack같음.
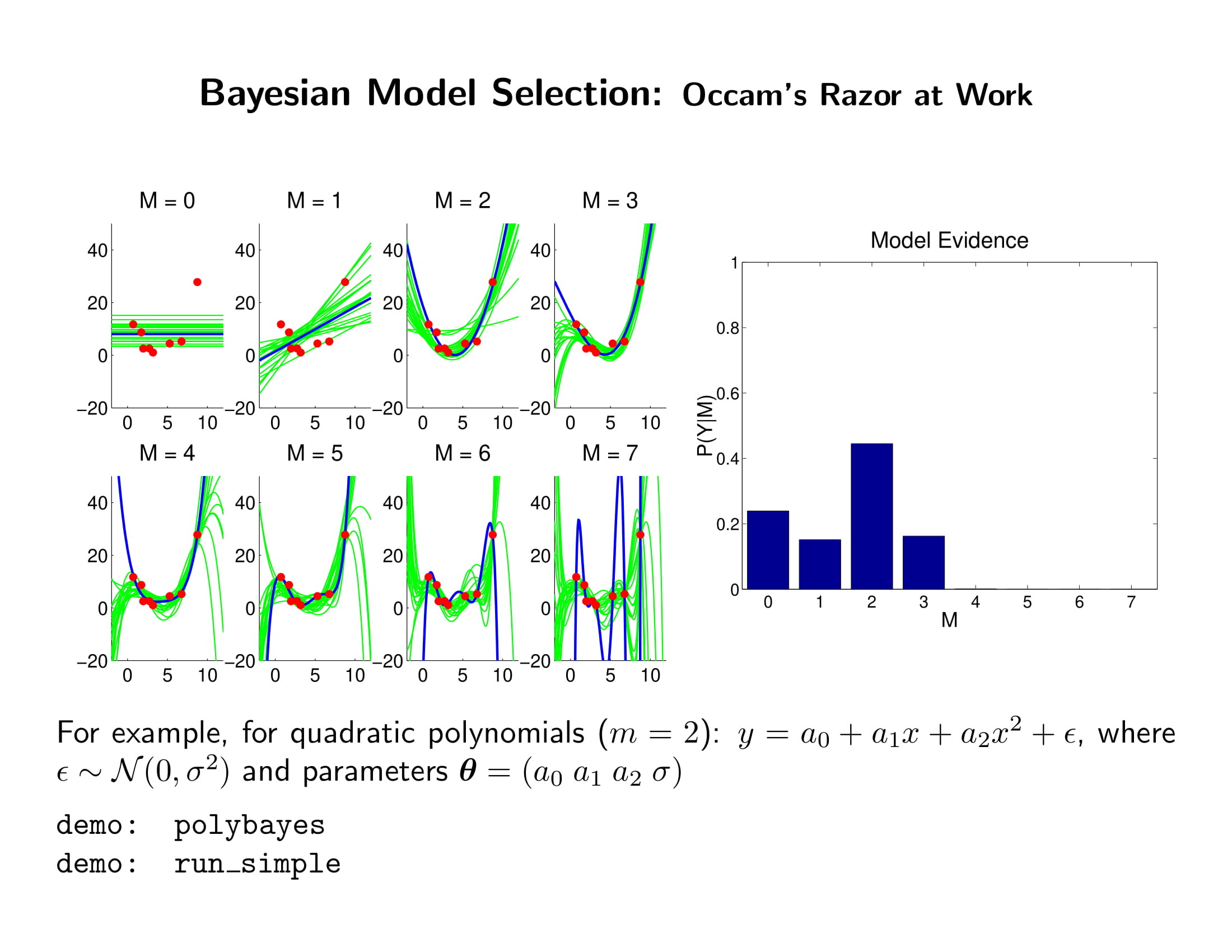
- 베타계수 노말, 분산 인버스 감마, full conjugate prior이라거 posterior에서 초록색 애들 바로 뽑을 수 있음.
- 코딩으로 직접 보일 수 있다. 언젠가 만들어서 블로그 올릴거임…

- hyperparameter의 역할은 parameter를 하나로 묶는 것이지, 거기서 더 계단을 올라가봤자 의미가 없다.
- hyperparameter에 넣을 값을 데이터를 보고 정하는게 empirical bayes
- 블로그에 Hierarchical Model에 대한 포스팅이 있으니 참조해보자.

- prior는 우리의 믿음을 최대한 반영해야함. 그럼 어떻게 반영하냐? 도메인 지식이 중요하겠지.
- 그냥 겸손하게 not too ridiculous한 파라미터의 range를 가져오는 것도 belief라고 볼 수 있음. subjective prior라고 해서 크게 겁먹을 필요가 없음.
- 그렇게 만든 prior를 어떻게 평가한가? prior에서 데이터를 만들어보고 그 결과를 함 보자. 데이터에 맞추는 게 아니라 상식적으로 그 자료의 성격에 맞아야 한다는 것. 예컨대 자료가 사람의 키인데 내가 만든 prior에는 키가 막 3m인 애들도 우수수 나오면 prior 설정이 잘못된거임
- 결국 prior가 어쨋든 간에 베이지안의 핵심은 averaging이니 크게 신경 노노!

- 먼저 데이터를 보고 hyperparameter를 정한다는게 사실 컨닝하는 거라서, 막 내가 전혀 예상하지 못했던 데이터가 와도 모델이 데이터를 잘 설명하게 되는 장점이 있긴 함. 그래서 robust하다고도 하는데
- 그런데 데이터에 잘 맞는다는 것은 그만큼 overfitting하게 되는 거임. 데이터를 보고 hyperparameter를 정하고 또 그 모델을 data로 학습시키는 것이니 double counting
- 그러나 한 두 개 정도는 이렇게 해도 overfitting이 그렇게 심각하지는 않음
- $\theta$의 MLE를 찾는게 Level 1 ML

-
지수분포족의 덴시티에서 데이터와 파라미터의 관계는 지수항 안에서 선형으로 이뤄짐
-
$\phi$를 natural parameter, $s(x)$를 sufficient statistics이라고 함. 예컨대 Gaussian에서 natural parameter는 $\mu, \sigma^2$의 reparameterization $$ \begin{align} p(x\mid \mu, \sigma^2) &\propto \exp{-\dfrac{1}{2\sigma^2}\sum_{i=1}^n(x_i-\mu)^2}\
&\propto \exp{-\dfrac{1}{2\sigma^2}\sum_{i=1}^nx_i^2+\dfrac{\mu}{\sigma^2}\sum_{i=1}^n x_i }\
&= \exp{ \begin{bmatrix} -1/2\sigma^2 & \mu/\sigma^2 \end{bmatrix} \begin{bmatrix} \sum_{i=1}^nx_i^2 \ \sum_{i=1}^nx_i \end{bmatrix}} \end{align} $$ -
위에 $p(x\mid \theta)$는 $x$에 대한 pdf인데 $p(\theta)$는 $\theta$에 대한 pdf이지만 둘의 형태가 같음
-
때문에 conjugate prior는 posterior가 그냥 모수 hyperparameter만 업데이트하는거임 $$ \begin{align} \eta &\to \eta + N\
\nu &\to \nu+\sum_n s(x_n) \end{align} $$- conjugate prior를 쓰는 이유: 간편하니까! 그리고 지수분포족 prior가 모수의 영역에 확률을 적당히 뿌리기에 좋음. 어차피 믿음만 제대로 표현할 수 있으면 되니까 이왕이면 편하게 conjugate한 애들 쓰는거임. 믿음을 있는 그대로 표현해야지 왜 지수분포족으로 타협하냐고? 아니 이거만 써도 믿음을 충분히 뿌릴 수 있다니까..?

- 이미 봤지요?
- 여기서 가장 구하기 어려운게 $p(\mathcal{D}\mid m)$ marginal likelihood, 우리가 모델을 $m$이라고 특정해서 그렇지 그냥 베이즈 룰에서 보는 $p(\mathcal{D})$를 말하는거임

- 왜 어렵냐고?
- $p(\mathbf{y}\mid m)$의 적분이 엄청 고차원인 경우가 많음. 모수 개수가 많을수록 모수 개수만큼 n중적분을 해줘야 함
- 심이저 latent variable $\mathbf{x}$의 존재를 가정하면 얘네들에 대해서도 적분을 해야함
- 애초에 Likelihood 자체가 계산이 너무 복잡한 경우도 많음
- 때문에 이 marginal likelihood와 posterior를 우회하여 구하는 방법이 수십 년 동안 연구가 됨. 우리가 배울 내용들임

- optimization 문제의 해결을 위해 여러 알고리즘이 있는 것처럼 marginalization 문제의 해결을 위해서도 여러 알고리즘이 있음
- 각각의 알고리즘은 모두 speed - accuracy tradeoff 관게에 있다.

-
PRML에 자세히 나옴. 한 마디로 posterior를 MAP에서 정규근사하고 $p(\mathbf{y}) = \dfrac{p(\boldsymbol{\theta})p(\mathbf{y} \mid \boldsymbol{\theta}) }{p(\boldsymbol{\theta}\mid \mathbf{y})}$를 이용해 marginal likelihood에 넣는 것임
-
아까 posterior 분포는 $n\to \infty$에 따라 참 모수 $\boldsymbol{\theta}^{true}$에서의 디락 델타 펑션이 된다고 했는데, 그 수렴하는 과정이 정규분포라고 볼 수 있다고 해보자. 엄밀하지는 않음
-
$n$이 크다는 것은 $\hat{\boldsymbol{\theta}}=\boldsymbol{\theta}^{MAP} \to \boldsymbol{\theta}^{true}$이니까 수렴하는 과정이라는 것. 때문에 posterior를 $\boldsymbol{\theta}^{MAP}$를 중심으로 한 정규분포로 근사할 수 있음
-
이 식의 근본이 뭐냐? 다음과 같이 어떤 pdf의 상수배만 알고 있을 때
-
이때 postive matrix인 $A$가 symmetric definite하려면 (그래야 정규분포가 well-defined되니까) Hessian인 $\nabla\nabla f(\boldsymbol{\theta})\mid_{\boldsymbol{\theta}=\hat{\boldsymbol{\theta}}}$의 모든 원소가 0보다 작아야 하며, 이는 즉 포스테리어에서 MAP가 saddle point같은 게 아니라 local maximum이어야 한다는 것을 의미함.
(출처: PRML, p.215)
-

-
Laplace Approximation에서 계산이 빡센 부분은 행렬식을 구하는 것. $d\times d$ 행렬의 행렬식을 구하는 데에는 대략 $d^{3.2+o(1)}\approx d^3$번 연산이 필요. (참조)
-
아 행렬식 구하는거도 힘들다. 그럼 BIC 쓰는거임
- Laplace Approximation의 식에서 $n$에 의존하지 않는 애들은 다 날려버리자. 그럼 프라이어, 상수항 다 날라감.
- Likelihood $\ln p(\mathbf{y}\mid \hat{\boldsymbol{\theta}})$는 데이터 개수 $n$에 따라 linear하게 증가함. iid 샘플이면 $\ln p(\mathbf{y}\mid \hat{\boldsymbol{\theta}})$는 개별 데이터 $y_i$의 로그우도의 합이니까.
- $-A=\nabla\nabla\ln p(\boldsymbol{\theta})p(\mathbf{y}\mid \boldsymbol{\theta})\mid _{\boldsymbol{\theta}=\hat{\boldsymbol{\theta}}}$도 자세히는 안 보이지만 $n$에 따라 linear하게 증가함. 그러면 $d \times d$행렬이니까 $\mid A\mid$는 $n^d$만큼 증가함. 그래서 로그 씌우면 대충 $\ln \mid A \mid \approx d\ln n$ as $n \to \infty$.
-
prior에 의존하지 않으니까 MAP 대신에 MLE 써도 됨
-
Minimum Discription Length Criterion하고 똑같음. 그게 뭔데..
-
문제는 BIC 식에서 model complexity가 parameter의 개수로 표현이 되어있다는 건데, 모수의 개수와 model complexity가 항상 같이 가는 것은 아님. 모수가 적어도 엄청 복잡한 모델이 얼마든지 있을 수 있고, 간단한 모델이어도 모수가 무한대일 수 있음. 그래서 전반적으로 모수 개수로 모델 복잡도를 말하는 것은 안 좋음
- 다만 모델이 identifiable하다 등의 여러 가정이 충족될 때 “점근적으로는” 위처럼 BIC로 model evidence를 근사하는 접근이 설득력이 있음.
- identifiable하다는 조건은 극한에서 modal이 하나밖에 없어야 하는 것.

-
marginal likelihood를 바로 못 구하면 lower bound라도 구해보자. 그래서 lower bound끼리 대소를 비교해 모델을 비교해보자.
-
$\boldsymbol{x}$를 어떤 잠재변수라고 하자. 위에 부등식이 성립하는 이유는 Log가 concave하기 때문이다. 즉 평균의 로그값이 로그값의 평균보다 크기 때문. 젠센의 부등식에 의해
-
만일 $q$가 간단해서 $\boldsymbol{x, \theta}$의 식으로 각각 깔끔하게 나눠질 수 있다면, $q_{\boldsymbol{\theta}}(\boldsymbol{\theta}), q_{\boldsymbol{x}}(\boldsymbol{x})$를 순차적으로 update하면서 $\mathcal{F}_m$의 값을 최대화하는 알고리즘을 생각할 수 있는데, 그게 바로 EM 알고리즘!

- Variational Bayes에 대한 자세한 내용은 PRML 10장을 공부할때 글을 써보겠다!


-
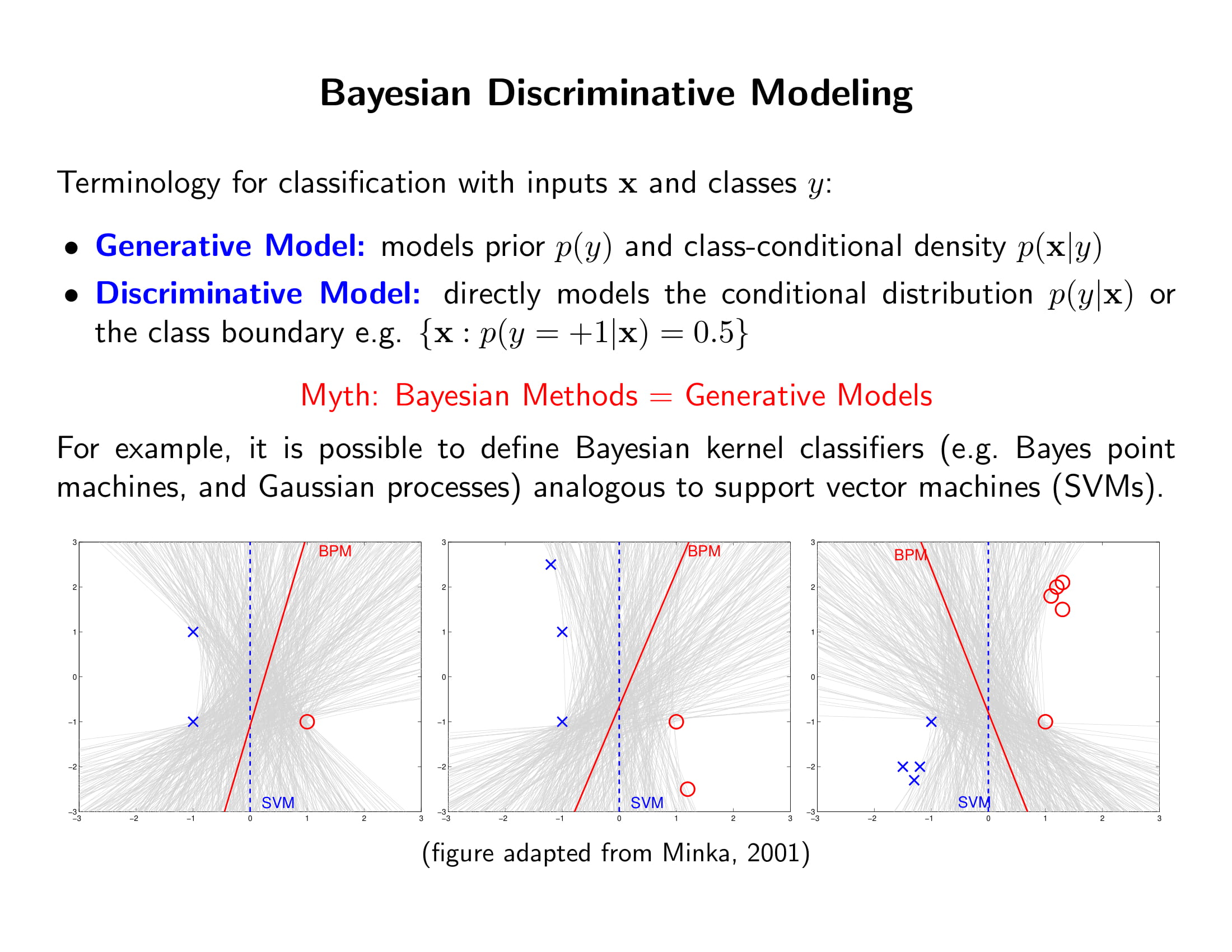
저번 학기에 다 본 내용이긴 한데 잠깐 복기하자면, $x$를 보고 $y \in {-1, 1}$를 결정하는 Binary Classification 문제에서 확률 모델 $p(y=1\mid x)$을 짜는 방법은 두 종류가 있음.
- Generative Model: $p(y=1\mid x)=\dfrac{p(y=1)p(x \mid y=1)}{p(x)}$으로 봐서 $p(y)$와 $p(x\mid y)$을 추정하는 모델. Naive Bayes Classifier, LDA, QDA 등이 있음
- Discriminative Model: $p(y=1\mid x)$을 바로 모델링하는 방법. 대표적인게 Logistic Regression.
-
Generative Model은 베이즈 정리를 사용하긴 하나 베이지안 방법은 아니다. 베이지안 방법의 핵심은
- 하나의 답을 내지 않고 가능한 모든 답의 분포를 보여주며
- 그 가능한 모든 답의 분포의 평균을 사용한다 (averaging) 는 것.
그러나 예컨대 Naive Bayes Classifier같은 경우는 하나의 classifier만을 보여줄 뿐임.
-
베이지안 classifier의 예로는 Bayes Point Machines가 있음. 이를 SVM (Maximal Margin Classifier)하고 비교해보면
- SVM은 마진에 위치한 점들 (support vectors) 만을 고려하여 이 점들로부터 마진이 최대가 되는 하나의 hyperplane만을 제시함.
- 그러나 위의 그림처럼 (설명의 단순화를 위해 linear classifiable한 경우만 보자면) 두 클래스를 나누는 hyperplane은 회색선으로 정말 많음. BPM은 이 많은 선들이 (위의 경우 하나의 직선은 절편과 기울기, 두 모수로 결정되니까 모수 공가이 2차원) 균일 분포를 이룬다고 가정하고, 이 분포의 평균을 쓰는 거고, 그게 BPM
- 그러면 SVM이 딱 마진에 있는 벡터들에만 의존하는 것과 달리 BPM은 마진 뒤에 있는 벡터들에도 영향을 받게된다. Sparse하진 않지만 위의 그림처럼 좀 더 데이터의 퍼짐을 잘 반영하는 classifier를 그릴 수 있는 것.

- 데이터에 담긴 모든 정보를 유한 차원의 모수로 압축하는 방법이 parametric 방법임. 즉 과거의 데이터와 현재의 데이터를 연결하는 유일한 information channel이 바로 $\boldsymbol{\theta}$. 때문에 모델의 복잡도가 제한되어있는데, 데이터의 양이 무제한으로 커질 수도 있는데 이렇게 복잡도를 제한하는 것은 그렇게 유연한 방법은 아님. 데이터에서 오직 제한된 정보만 얻을 수 있기 때문. 비모수적 방법은 모수적 방법의 정반대.
- 모수적 방법은 과거 데이터의 모든 정보가 모수의 값에 다 반영되기 때문에 model-based임. 즉 뭐냐면 모수의 추정치 혹은 분포만 알고나면 그 학습을 위해 썼던 데이터가 필요가 없다는 것임. 그러나 비모수적 방법은 데이터에 담긴 정보를 모두 그대로 사용하기 때문에 모델을 순차적으로 업데이트하기 위해서는 이전에 쓰인 모든 데이터를 다 알아야함. 즉 memory-based
- 근래 머신러닝에서 성과를 많이 거둔 알고리즘들은 svm 등 kernel based methods나 뉴럴 네트워크 이런 애들은 다 nonparametric한 방법들이었음 (그도 그럴만한게 데이터가 엄청 많으면 당연히 비모수 방법이 유리하지 모델이 제한되어 있지 않으니까. 못 알아먹어서 문제지만.)
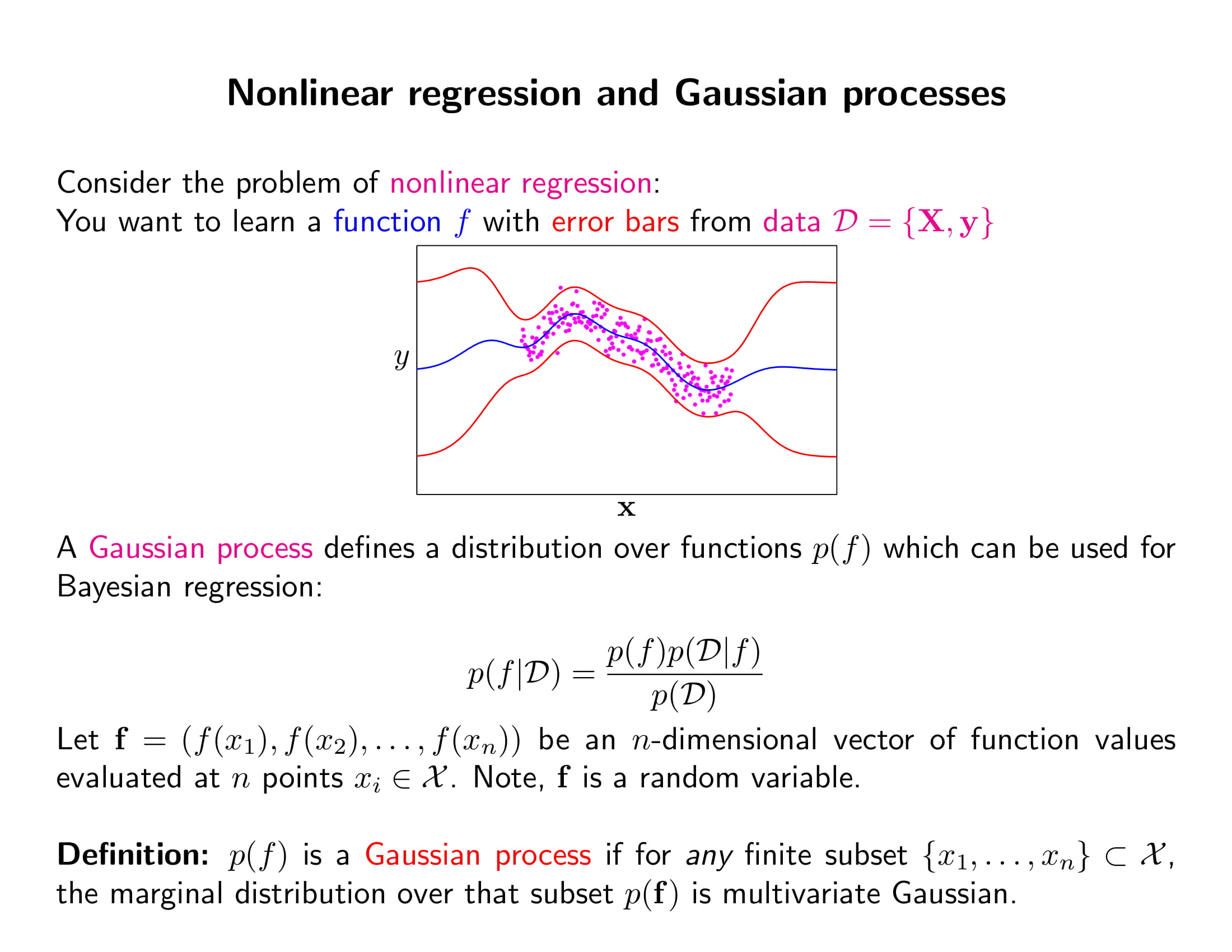
- skip
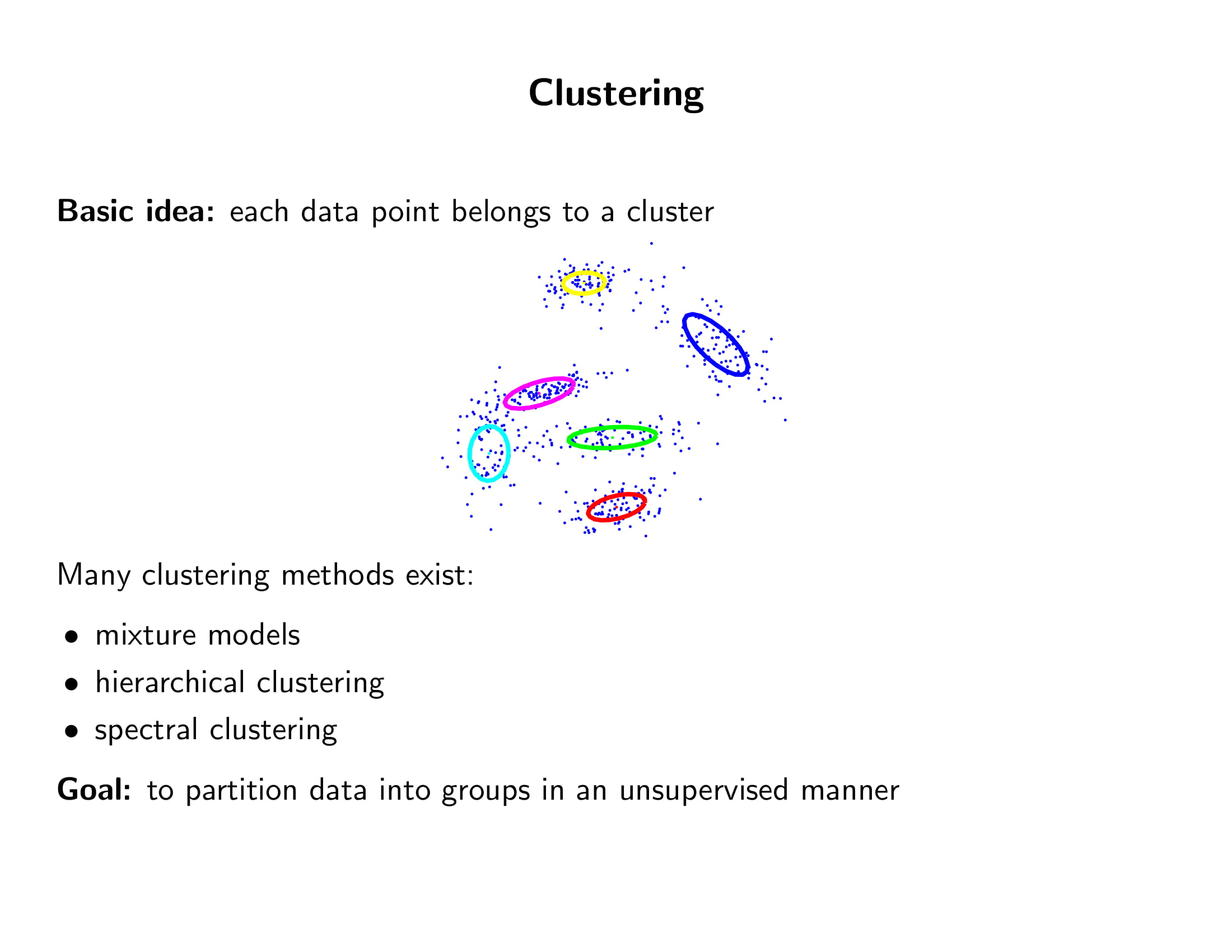


- Gaussian Mixture인데 클래스 개수가 무한히 확장 가능하면 (즉 미리 정해지지 않았다면) 그걸 Dirichlet Process Mixtures라고 하나보다. 다음 시간에 할거다.

- 이거 다 다음시간에 할건데, 한가지 중요한 것은 모델과 알고리즘은 다르다는 것.
- 모델은 데이터 형성 과정에 대한 설명. 위의 경우 저 모델은 Dirichlet Process Mixtures이고, 저 모델을 학습하는 방법이 바로 EM 알고리즘 등등이다.

- 다음에 이어지는 것은 그냥 읽어보자. 아조시가 베이지안 머신러닝 전공하면서 듣다가 빡친 소리들 모아놔서 하나씩 까는 것 같다.

- MAP는 사실 그냥 Regularization같은 느낌이 강함. 베이즈 방법의 핵심은 averaging임. 그리고 MLE는 reparameterization에 invariant하지만, MAP는 reparameterization에 variant하다. 그래서 MAP 쓸 바에야 그냥 MLE 써라. Regularization같은 효과를 보고 싶으면 그냥 굳이 prior 갖고 오지 말고 regularization을 바로 써라.

- 베이지안 추정량에 frequentist 기준을 들어 평가할 수도 있음.
- 뭐 optimization보다는 averaging이 어렵긴 한데… 꼭 불가능한 것도 아님.




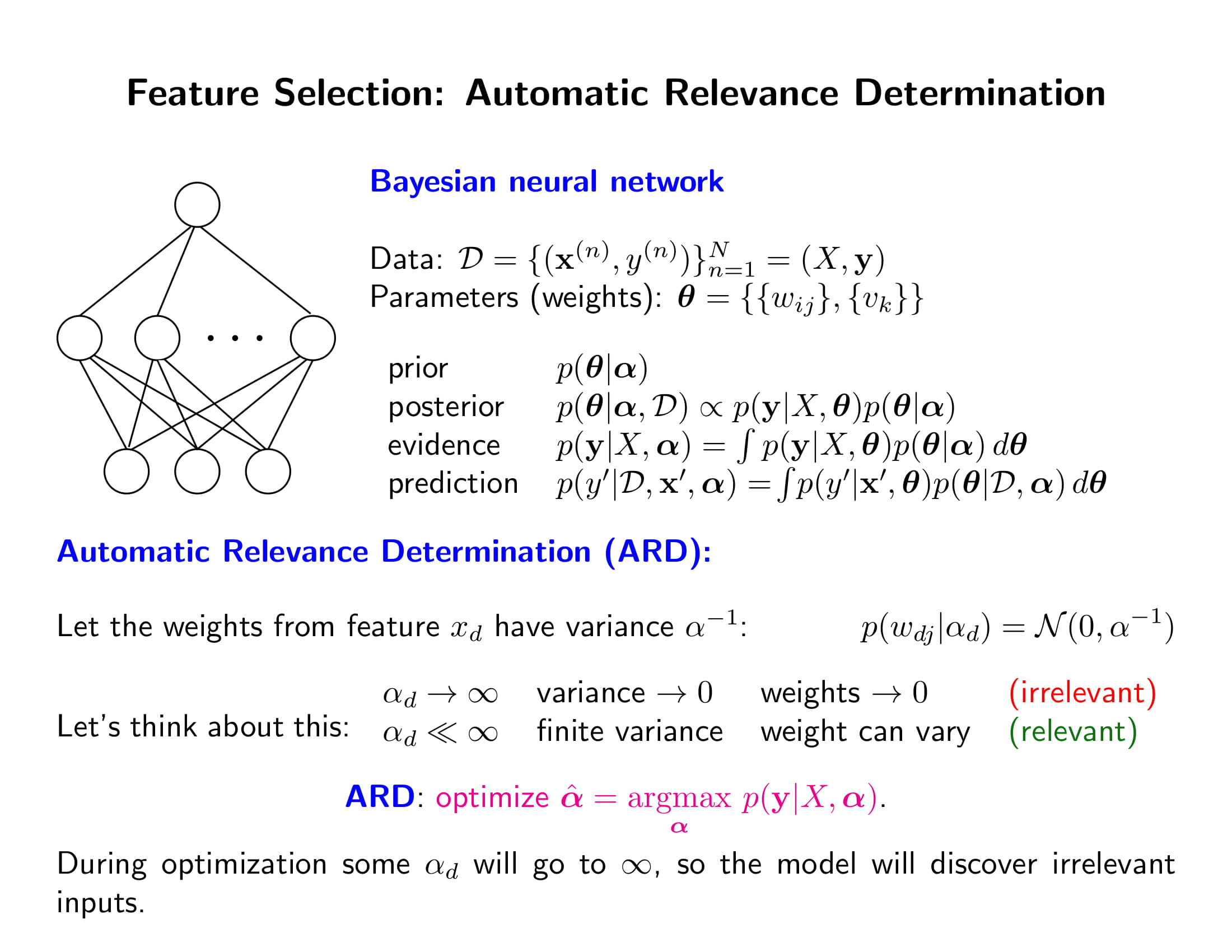
지금부터 나오는 내용은 강의에도 다루지 않은 부분이다. 이런 주제도 있구나 하고 고개를 끄덕이거나 갸우뚱하고 넘어가자.












References
- http://videolectures.net/mlss2012_ghahramani_bayesian_modelling/
- Pattern Recognition and Machine Learning, Bishop, 2006
- http://krasserm.github.io/2019/02/23/bayesian-linear-regression/

