06 Maximum Likelihood Theory

지금까지의 논의를 종합해보면 다음과 같습니다.

1. 빈도통계학 추론은 평행우주 데이터 ${D^{(s)}}_{s=1}^{\infty}$에서의 Sampling Distrubtion $\delta(D^{(s)}) \sim p(.\mid \theta^*)$에 달렸다.

2. 모수 $\theta$에 대한 추정량 $\hat{\theta} = \delta(D^{(s)})$의 결정은 다음의 사항을 고려해야 한다.

   1. 일단 $\delta$의 sampling distribtion을 근사적으로나마 알아야 한다.

   2. 가급적이면 $\delta$의 평행우주 데이터 ${D^{(s)}}_{s=1}^{\infty}$에서의 행태가 “이쁘면” 좋겠다. (Consistent, Unbiased, Efficient)

3. Sampling distribution $\delta(D^{(s)}) \sim p(.\mid\theta^*)$만 알면 점 추정, 구간 추정, 가설 검정 다 할 수 있다!

빈도통계학 추론에서 제일 “빡센” 부분은 바로 2-1. 입니다. 데이터에 대한 Likelihood 모형을 세우고 이를 바탕으로 모수에 대한 추정량 $\delta$을 결정했는데, 여기서 $\delta$의 극한 분포를 유도하는 과정이 여간 힘든게 아니라고 합니다. (해석학이 필수인 이유 중 하나입니다.) 이를 구하는 방법은 크게 다음과 같습니다.

1. Plug-in Principle: 우리가 매일 처음 봤던 예시가 중심극한정리와 슬러츠키 정리인데, 이처럼 추정량 안에 있는 nuisance parameter를 표본에서 계산한 값으로 떄려넣는 것을 plug-in한다고 합니다.

2. Taylor-series Approximation: 수통1에서 배운 delta-method입니다. 어떤 모수 $\theta$의 추정량 $\hat{\delta}$의 극한분포를 이미 알고 있을 때, 그 모수의 함수 $g(\theta)$의 극한분포를 구하는 방법입니다. 함수 $g$를 $\hat{\theta}$ 근처에서 선형근사 (테일러 1계 근사)하여 다음과 같이 나타냅니다.

3. Maximum Likelihood Theory: 이제 얘기할 내용입니다. 결론부터 스포하자면 모수가 있는 분포함수족에 대해서 Likelihood를 최대화하는 모수를 $\hat{\theta}_{mle}$라고 할건데, 다음과 같은 극한분포를 가집니다.

4. (Non-parameteric) Bootstrap: 컴퓨터 연산력도 썩어나겠다 내가 그냥 $D_{s=1}^{\infty}$를 손수 만들어서 추정량 $\delta$의 분포를 직접 보겠다는 방법입니다. 쉽게 말하면 데이터의 크기가 충분히 크면 데이터의 경험분포 (그러니까 히스토그램)이 실제 분포 $f(D\mid\theta)$를 잘 근사할 것이니, 데이터에서 표본 크기만큼 다시 **복원추출**하여 $S$개 만큼의 인위적인 데이터의 앙상블 $D_{s=1}^{\infty}$을 만들겠다는 이야기입니다. 극한분포를 진짜 죽어도 못 구해서 어쩔 수 없을 때 울며 겨자먹기로 논문에 쓰는 방법이라고 들었습니다.

그럼 지금부터 3번 Maximum Likelihood Theory에 대해 알아보겠습니다.

Maximum Likelihood Theory 수식으로 보이기

자 먼저 빈도론자들 세계관부터 다시 써봅시다.

$$ \begin{align} \text{Ensemble of Data:}\quad & D_{s=1}^{\infty} = [x_1^{(s)}, x_2^{(s)}, …, x_n^{(s)}]_{s=1}^{\infty}\\\
\text{Sampling Density of $D^{(s)}$ (iid):}\quad& f(D^{(s)}|\theta) = \prod_{i=1}^nf(x_i^{(s)}|\theta) \quad (x_i^{(s)}\in \mathcal{X}, \theta \in \Omega)\\\
\text{Likelihood of $\theta$ given $D^{(s)}$:}\quad& L(\theta|D^{(s)}) \end{align} $$ 여기서 모수의 추정량을 결정할 때 다음과 같은 추정량을 생각할 수 있습니다.

$$ \begin{align} \text{True (fixed) Parameter}:&\quad \theta\\\
\text{Estimator of $\theta$ given $D^{(s)}$:}& \quad \delta(D^{(s)})= \arg\max_{\theta} L(\theta|D^{(s)}) \end{align} $$ 즉 데이터로 결정되는 $\theta$의 함수인 Likelihood에서, 함수의 값 $L(\theta \mid D^{(s)})$이 가장 큰 지점을 $\delta$로 정하는 것입니다. 이 추정량을 $\hat{\theta}$이라고 합니다. 뭔가 직관적으로 크게 이상하지는 않아요. 비록 $p(D^{(s)}\mid\theta)$는 모르지만, 적어도 우리가 가진 데이터에서는 $\theta=\hat{\theta}$일 때 $p(D^{(s)}\mid\theta)$의 값이 가장 크니까, 데이터에 가장 잘 들어맞는 값이라고 생각할 수 있으니까요. Maximum Likelihood Theory는 현대통계학의 천재 (그러나 본인이 애연가시라 흡연과 폐암의 관계는 한사코 부정하신(사실 Randomized된 실험 결과가 없으니까)) 로날드 피셔께서 그냥 혼자서 뚝딱 다 만들었는데, 피셔 이전에도 대충 이런 생각으로 MLE를 쓰자고 제안한 사람은 많았지만, MLE의 극한분포를 제시한 분이 바로 피셔입니다.

사실 MLE는 Likelihood를 최대화하는 값이므로 단조변환인 로그변환을 하면 log-likelihood를 써도 됩니다. 그렇게 되면 최대화 문제가 훨씬 더 쉬워집니다.

$$ \theta_{mle}=\arg\max_{\theta} L(\theta\mid D^{(s)}) = \arg\max_{\theta} l(\theta\mid D^{(s)}) = \arg\max_{\theta}\sum_{i=1}^n \log f(x_i^{(s)}\mid\theta) $$

이제 MLE의 행태를 살펴보면서 MLE 사용에 대한 정당화 근거를 간단히 알아보겠습니다. 그 전에 몇 가지 개념을 짚고 넘어갈게요.

• Log Likelihood: 말 그대로 Likelihood에 로그를 취한 함수입니다. (로그 우도)

$$ \begin{align} l(\theta | x_i) = \log f(x_i|\theta) \end{align} $$

• Score Function: Log likelihood을 모수 $\theta$에 대해 미분한 함수입니다. 모수가 벡터일 경우 로그 우도의 gradient로 정의합니다. score function이 말하는 바는 “로그 우도의 기울기"입니다.

  $$ \begin{align} s(\theta|x_i) &= \dfrac{d}{d\theta};l(\theta|x_i) \quad (\theta \in \mathbb{R})\
  &= \nabla_{\theta}; l(\theta|x_i) = [\dfrac{\partial ;l(\theta|x_i)}{\partial \theta_1}, \dfrac{\partial ;l(\theta|x_i)}{\partial ;\theta_2}, …, \dfrac{\partial; l(\theta|x_i)}{\partial \theta_d}] \quad (\theta\in \mathbb{R}^d) \end{align} $$ n개의 iid 데이터로 이뤄진 $D^{(s)}$의 로그 우도는 개별 데이터의 로그 우도의 합으로 이뤄짐을 보았습니다. 때문에 $D^{(s)}$의 score function은 다음과 같습니다.

  $$ \begin{align} s(\theta|D^{(s)}) = ns(\theta|x_i) \end{align} $$

• Fisher Information: Score function도 또한 데이터의 함수 $s(\theta \mid x_i)$입니다. 때문에 모수값이 어떤 $\theta$로 주어지면 $x_i \sim f(x_i\mid\theta) $의 분포를 따르며, 데이터의 통계량인 $s(\theta \mid x_i)$의 평균과 분산을 계산할 수 있습니다. 이때 score function의 평균은 0이며, 분산을 Fisher Information $I(\theta)$이라고 합니다. 데이터가 n개인 경우도 위와 마찬가지로 쓸 수 있습니다.

  $$ \begin{align} E_{x_i|\theta}[s(\theta|x_i)] &= E_{x_i|\theta}[\dfrac{d;l(\theta|x_i)}{d \theta}] = \int \dfrac{f'}{f}fdx=\dfrac{d}{d\theta}\int f dx=0 \quad (\theta \in \mathbb{R}^1)\\\
  E_{x_i|\theta}[s(\theta|x_i)] &= \mathbf{0} \in \mathbb{R}^d \quad (\theta \in \mathbb{R}^d) \end{align} $$

Fisher Information은 다음과 같이 score function으로 나타낼 수 있음을 어렵지 보일 수 있습니다. (이런 걸 다 수통 2때 합니다)

$$ \begin{align} I(\theta)&=V_{x_i|\theta}[s(\theta|x_i)] = -E_{x_i|\theta}[s(\theta|x_i)^2] = -E_{x_i|\theta}[s'(\theta|x_i)] \\\
I_n(\theta)&=V_{D^{(s)}|\theta}[s(\theta|D^{(s)})] = nV_{x_i|\theta}[s(\theta|x_i)] = nI(\theta) \end{align} $$

Fisher Information이 말하는 바는 “어떤 지점 $\theta$에서 로그 우도의 peak한 정도"입니다. 로그 우도 함수가 뾰족하다는 것은 그만큼 데이터가 $\theta_{mle}$에 많이 쏠려있다는 것이고, 여기에서 즉 모수의 추정량으로서 MLE의 분산이 작을 것을 기대할 수 있습니다.

(모수가 벡터인 경우 Fisher Information Matrix을 다음과 같이 정의할 수 있으며, 아래의 등호가 성립함을 어렵지 않게 보일 수 있습니다.)

$$ \begin{align} I(\theta)_{k,j} = Cov(\dfrac{\partial l(\theta|x_i)}{\partial \theta_k}, \dfrac{\partial l(\theta|x_i)}{\partial \theta_j}) = E[-\dfrac{\partial^2 l(\theta|x_i)}{\partial\theta_k\partial\theta_j}] \end{align} $$

이제 단일 모수인 경우에 대해 간단하게 MLE의 극한분포를 증명해보겠습니다. 우선 score function에 대하여 다음과 같이 테일러 1계 근사 식을 쓸 수 있습니다.

$$ \begin{align} 0 = s(\theta_{mle}|x_i) \approx s(\theta^*|x_i) + s'(\theta^*|x_i)(\hat{\theta}_{mle} - \theta^*) \end{align} $$

score function은 정의상 MLE에서 0입니다. 이때 score function을 MLE에 대한 함수로 보고, MLE 근처에 있을 것만 같은 참 모수값 $\theta^*$에서 이 함수 $s(\hat{\theta}_{mle}|x_i)$를 선형근사해본 것입니다. 그러면 위 식을 다시 아래처럼 쓸 수 있습니다.

$$ \begin{align} \hat{\theta}_{mle} \approx \theta^* + \dfrac{s(\theta^*|x_i)/n}{-s'(\theta^*|x_i)/n} \end{align} $$

• $s(\theta \mid x_i)/n$ 이 식은 score function의 평균입니다. score function의 평균은 0이며, 분산은 $I(\theta)$입니다. 때문에 중심극한정리에 의해 $s(\theta\mid x_i)/n \sim^A N(0, I(\theta)/n)$으로 쓸 수 있습니다.
• 위에서 이미 $I(\theta)= -\mathbb{E}_{x_i\mid\theta}[s'(\theta\mid x_i)]$임을 보였습니다. 때문에 대수의 법칙에 의해 $-s'(\theta\mid x_i)/n$은 $I(\theta)$으로 확률 수렴합니다.

이걸 다 종합해보면, 그리고 슬러츠키 정리를 사용해 모르는 참모수 $\theta$을 $\hat{\theta}_{mle}$으로 plug-in 하면, 우리는 다음과 같은 MLE의 극한 분포를 얻을 수 있습니다.

$$ \begin{align} \text{Single parameter}&\quad \hat{\theta}{mle} \sim^A N(\theta^*, \dfrac{1}{nI{\hat{\theta}{mle}}})\\\
\text{Multi-parameter}&\quad \hat{\theta}{mle} \sim^A N(\theta^*, \dfrac{1}{n}\mathbf{I}^{-1}(\hat{\theta}_{mle})) \end{align} $$ 즉 모든 Likelihood 모델에 대하여, 여기에서 말하지는 않았지만 이 함수들이 어떤 정규성 가정들을 만족한다면 (지수분포족이면 충분히 만족하는), 우리는 Likelihood를 최대로 하는 추정량의 극한분포가 정규분포라는 것을 알 수 있습니다. 이 놀라운 결과를 바탕으로 아까 봤던 빈도통계학의 추론을 똑같이 다 할 수 있는 것입니다. (Likelihood를 이용한 검정 방법은 따로 소개하지 않겠습니다. 링크 참조)

간단하게 말하면 Likelihood에서 귀무가설 $\theta_0$와 데이터의 추정량, 예컨대 MLE $\hat{\theta}_{mle}$ 간의 scaled된 거리를 보는 것이 Wald Test, 두 지점에서의 높이의 차이를 보는 것이 Likelihood Ratio Test, 그리고 귀무가설 지점에서의 기울기를 보는 것이 Score Test입니다. 귀무가설 지점의 위치에 따라서 다소 차이가 있어도 결국은 똑같은 Likelihood 함수에서 $x$축에서의 차이를 볼거냐, $y$축에서의 차이를 볼거냐, 아니면 기울기를 보느냐의 차이기 때문에 결과는 크게 다르지 않습니다. 위 링크에 있는 그림을 보면 이해가 될 거 같아요.

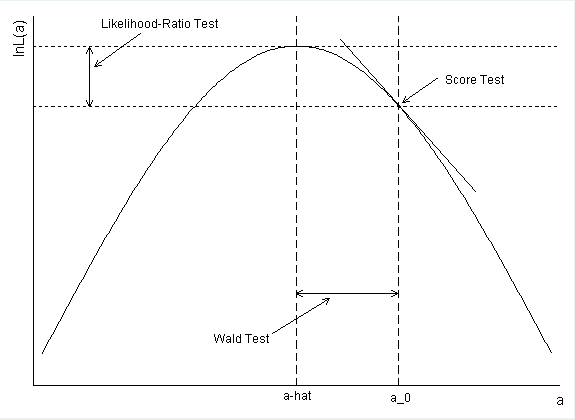
(출처: 링크)

MLE는 점근적으로 Minimum Variance인 Unbiased Estimator입니다. MLE 극한분포의 분산은 Rao-Cramer lower bound에 의하면 모든 불편추정량이 가질 수 있는 분산의 하한입니다. 또한 MLE는 항상 평균이 모수와 일치하지는 않지만, 그 편차가 점근적으로 0이 되므로 점근적으로 Unbiased라고 볼 수 있습니다. 이처럼 MLE는 굉장히 훌륭한 빈도통계 추정량 성질을 가지고 있으며, Likelihood만 있으면 Test를 위한 검정통계량의 극한분포도 알려져 있기에, 사실상 거의 모든 빈도통계 추론은 MLE와 LRT로 이뤄진다고 봐도 과언이 아니겠습니다.

References

1. Probability Theory and Statistical Inference: Econometric Modeling with Observational Data (Spanos, 1999)
2. Machine Learning: a Probabilistic Perspective (Murphy, 2012)
3. Computer Age Statistical Inference (Efron, Hastie, 2016)
4. Calibration of p Values for Testing Precise Null Hypotheses (Sellke et al, 2001)
5. https://ocw.mit.edu/courses/mathematics/18-05-introduction-to-probability-and-statistics-spring-2014/readings/MIT18_05S14_Reading20.pdf