(MCMC) Discrete-Time Markov Chain with Finite State Space

0. 이걸 왜 배우는데?

저번 시간에 간략히 살펴본 Gibbs Sampler는 MCMC(Markov Chain Monte Carlo), 즉 마코브 체인을 이용한 Posterior 분포 시뮬레이션 방법 중 하나인데, 이 MCMC 방법들이 도대체가 왜 잘 먹히는 지를 알려면 아무래도 마코브 체인에 대한 배경지식이 필요하다. 어떤 분포를 MCMC로 근사한다는 것은 모수 공간의 어떤 포인트에서 다른 포인트로 총총 점프하는 그 과정을 “잘” 구현해서, 마치 그 샘플들이 내가 모르는 그 분포에서 나온 것과 같다고 퉁치는 거다.

MCMC 이름의 의미

1. Markov Chain: 어떤 지점에서 다른 지점으로 점프하는 과정을 마코브 체인으로 볼거다
2. Monte Carlo: 그 마코브 체인의 랜덤 샘플들을 무진장 찍어낼거다

때문에 MCMC의 핵심은 어떤 한 샘플에서 (모수로 이뤄진 벡터)에서 다른 샘플로 넘어가는 알고리즘이다. 우리는 이름에 마코브 체인이 붙은 거에서 알 수 있듯이 어떤 포인트에서 다른 포인트로 넘어가는 과정을 “확률과정”, 그 중에서도 마코브 체인이라고 간주하고, 마코브 체인 중에서도 기깔나게 깔쌈한 녀석인 “ergodic"한 마코브 체인으로 만들 것이다. 그러면 우리는 나중에 배울 정리에 의해 마코브 체인 샘플들의 히스토그램을 마치 모분포에서 나온 샘플들의 히스토그램과 같다고 퉁칠 수 있다. 여기서 어떻게 마코브 체인을 ergodic하게 만들 것인가가 바로 MCMC 샘플러의 정체성을 결정한다고 볼 수 있다.

마코브 체인 중에서도 MCMC의 이론적 토대가 되는 것은 1) 이산형 시간에 2) 취할 수 있는 상태가 finite한 마코브 체인이다. 뭔데 ㅆ덕아라고 생각할 수 있겠지만 나중에 자세히 설명할 것이니 걱정말라. 다만 우리가 MCMC를 정당화할 때 이런 Discrete & Finite한 마코브 체인을 이용하는 것에는 중요한 가정이 숨어있다는 것을 명심해야 한다. (놀랍게도 이 부분은 책이나 자료들에서 잘 설명이 안 되어있다. 본인도 구글에서 겨우 찾은 거임)

모수공간에 대한 MCMC 샘플링의 숨은 가정

1. Discrete (countable): 어차피 컴퓨터는 32bit, 64bit 컴퓨터는 기껏해야 한정된 자릿수만 처리할 수 있다. 때문에 실제 모수 공간이 연속이어도 그냥 마치 Grid처럼 discrete한 공간으로 봐도 무방하다.
2. Finite: 실제로 연속인 1차원 구간이나 n차원 실수 공간은 그 원소들을 셀 수 없기 때문에 무한하다고 봐야 한다. 근데 어차피 컴퓨터로 시뮬레이션 하는거고, 메모리가 한정되어있으니 1에서 말한 이유처럼 컴퓨터가 처리하는 모수 공간은 finite하다고 봐도 된다. (참고로 finite의 정의는 굉장히 자비롭다. 지구 상의 모든 분자의 수 혹은 우주의 별의 수처럼 엄청 큰 숫자도 그것보다 큰 숫자가 있다고 치면 finite하다.)

물론 continuous markov chain으로 state space가 infinite한 경우에도 MCMC의 알고리즘이 정당화되는지는 더 알아봐야 할 문제이나, 본인은 위의 가정을 충분히 납득하기 때문에 이는 다루지 않겠다. (그리고 시간이 없다..!)

1. Random Process

먼저 확률과정(랜덤 프로세스)란게 뭔지 간략히 짚고 넘어가자. 쉽게 말하자면 확률변수들에다가 예컨대 시간으로 인덱스를 붙이면 $X(t)$ 그게 확률과정이 된다. 만일 이때 시간이 첫 날, 둘째 날, 셋째 날처럼 이산형이면 Discrete-time 확률과정이 되는거고, 아니면 어떤 구간 내 임의의 실수이면 Continuous-time 확률과정이라고 하는거다. 수식으로 쓰면 다음과 같다.

$$ \begin{align} \text{Random Process:} &\quad {X_t, t\in J}\\\
\text{Discrete-time:} &\quad \text{J is a countable set, such as $\mathbb{N}$ or $\mathbb{Z}$}\\\
\text{Continuous-time:} &\quad \text{J is an interval on $\mathbb{R}$} \end{align} $$

감이 안 온다면 예를 들어보자.

1. ${N(t), t\in[9,16]}$: 오전 9시부터 오후 4시까지 은행에 방문한 (누적) 손님의 수
2. ${T(t), t\in [0, \infty)}:$ 서울 시 $t$에 따른 실시간 온도

학부에서 배우는 확률과정에는 Renewal Process, Poisson Process, Markov Chain, Gaussian Process 등 여러가지가 있는데, 이 중에서 우리는 Markov Chain에 대해 알아보겠다.

2. Discrete Time Markov Chain

2-1. Definiton

마코브 체인은 어떤 확률 시스템에서 “상태"의 전개를 모델링할 때 많이 쓴다. 특히 어떤 한 시점에서의 상태가 바로 직전 상태, 혹은 이전의 몇 단계까지의 상태에만 의존한다는 가정이 있을 때 적절하다. 먼저 정의부터 살펴보자.

Definition (Discrete Time Markov Chain) 이산형 확률과정 $\{X_n, n\in 0, 1,2,…\}$에 대해 $X_n$이 취할 수 있는 값이 $dom(X_n)=S\text{ (a countable set)}$라고 하자. 이 프로세스가 모든 $m$에 대해 다음의 조건을 만족하면 우리는 이를 Markov Chain이라고 부른다.

$$ p(X_{m+1}=j|X_m=i, \underbrace{X_{m-1}=i_{m-1},,…,X_0=i_0}_\text{useless}) = \underbrace{p(X_{m+1}=j|X_m=i)}_\text{transition probability} $$

만일 이때 $S$가 유한하다면 우리는 이를 finite Markov Chain이라고 부른다.

$X_n=j$라는 것은 $n$ 시기에 상태가 $j$에 있다는 말이다. 또한 위의 정의에서 $p(X_{m+1}=j|X_m=i)$의 의미는 현재 상태가 $i$일 때 다음 상태가 $j$일 확률을 얘기하는데, 이를 transition probability라고 한다. 마코브 체인은 현재 상태에서의 transition probability가 오직 직전 상태에만 의존하는 확률과정인데, 이를 이용하면 $n$기까지의 joint distribution을 다음과 같이 쓸 수 있다.

$$ \begin{align} p(X_n=i_n, X_{n-1}=i_{n-1},…, X_{0}=i_{0}) =& p(X_n=i_n|X_{n-1}=i_{n-1})\\\
&p(X_{n-1}=i_{n-1}|X_{n-2}=i_{n-2})\\\
&…p(X_1=i_1|X_{0}=i_{0})p(X_0=i_0) \end{align} $$

이처럼 마코브 체인은 현재와 과거, 현재와 미래 등 오직 쌍으로만 의존하기 때문에 pairwise dependent하다고 한다. 이때 이 transition probability가 시간 $m$에 따라서 변하지 않는다고 하면 참 편할 것 같다. 그래서 그렇게 가정한 마코브 체인을 homogeneous하다고 하며, 이걸 수식으로 다음과 같이 쓴다.

$$ p_{ij} = p(X_{m+1}=j|X_m=i) \quad ^\forall m \quad \text{(i: now, j: next)} $$

Example (Random walk): 마코브 체인의 대표적인 예로는 Random walk가 있다. 확률과정 $\{X_n, n=0,1,2,…\}$을 다음과 같이 정의하자.

1. $X_0=0$, $X_n = X_{n-1} + \xi_n$
2. $\xi_{i}=+1 ;\text{with $p$}, ;\xi_{i}=-1;\text{with $1-p$}$

그러면 이 랜덤워크의 transition probability는 다음과 같이 쓸 수 있다.

$$ p(X_{n}=j|X_{n-1}=i_{n-1}, …,X_{0}=i_{0})= \begin{cases} p &\text{if}\quad j=i_{n-1}+1\\\
1-p &\text{if}\quad j=i_{n-1}-1 \end{cases} $$

자세히 보면 랜덤워크의 transition probability는 오직 직전 상태 $i_{n-1}$이 뭔지에만 의존하는 것을 볼 수 있다. 때문에 랜덤워크는 마코브 체인인 것이다.

예컨대 총 $r$개의 state가 있다면 transition probability도 총 $r \times r$개 있을거다. 이걸 한눈에 보기 쉽게 행렬로 쓴 거를 transition probability matrix라고 부른다.

$$ P= \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1r}\\\
p_{21} & p_{22} & \cdots & p_{2r}\\\
\vdots & \vdots & \ddots &\vdots\\\
p_{r1} & p_{r2} & \cdots & p_{rr} \end{bmatrix} $$

행렬을 읽을 때 열 방향으로 현재의 상태, 행 방향이 다음 기의 상태로 읽으면 된다. transition matrix는 다음의 성질을 만족한다.

1. $1 \geq p_{ij} \geq 0 $ for all $i,j$
2. $\sum_{k=1}^r p_{ik} = \sum_{k=1}^rp(X_{m+1}=k|X_m=i)=1$

1은 확률이니까 당연한 소리고, 2는 현재 상태에서 다음 상태로 어디로든 가야 한다 정도로 받아들이면 되겠다. 즉 transition matrix의 각 행의 합은 $1$이어야 한다는 것. 이 두 성질을 만족하는 행렬을 stochastic matrix라고 하는데, 역으로 말하면 모든 stochastic matrix는 어떤 마코브 체인의 transition probability matrix라고 할 수 있다.

한번 예를 들어보자. $S={1,2,3}$인 마코브 체인에서 다음과 같이 transition matrix가 주어졌다고 해보자.

$$ P=\begin{bmatrix} 1/3 & 1/3 &1/3\\\
1/2 & 1/2 & 0\\\
1/4 & 0 & 3/4 \end{bmatrix} $$

이 행렬이 나타내는 마코브 체인을 아래처럼 그림으로 그려볼 수 있는데, 이런 그림을 state transition diagram이라고 한다. 각 노드가 상태를, 화살표가 전환확률을 나타낸다고 보면 된다.

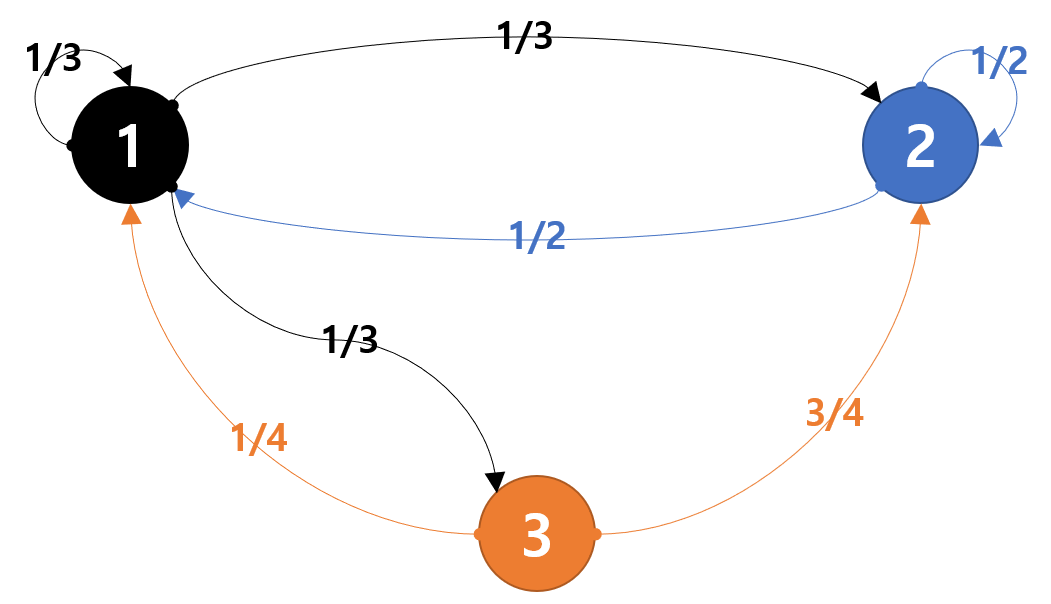
이처럼 마코브 체인은 행렬로도, 아니면 그림으로도 나타낼 수 있다. 앞으로 마코브 체인의 여러 성질을 이야기 할 때 이 그림과 행렬을 같이 보는게 이해에 좋다.

2-2. State Probability Distributions

1) One step transition probabilities

마코브 체인에서 우리가 궁금한 것은 어떤 시점에서 상태들의 분포일 것이다. 예컨대 확률과정 $\{X_n, n=0,1,2,…\}$의 state space가 $X_n \in S=\{1,2,…,r\}$이라고 해보자. 이때 처음 시점$(n=0)$에서 확률과정이 어던 상태를 취할 것인지 그 분포를 다음과 같이 써보자.

$$ \pi(0) = \begin{bmatrix} p(X_0=1) & p(X_0=2) & \cdots & p(X_0=r) \end{bmatrix} $$

그렇다면 다음 시기 $n=1, 2,…$에서 $\pi(1),\pi(2),…$는 어떻게 구할 수 있을까? 일단 전사건의 법칙을 이용하면 $p(X_1=j)$는 다음과 같이 써볼 수 있다.

$$ \begin{align} p(X_1=j) &= \sum_{k=1}^r p(X_1=j|X_0=k)p(X_0=k)\\\
&= \sum_{k=1}^r p_{kj}p(X_0=k) \end{align} $$

때문에 다음 기의 확률분포 $\pi(1)$는 다음과 같이 간단히 벡터와 행렬의 곱으로 나타낼 수 있다.

$$ \begin{align} \pi(1) = \pi(0)P =&\begin{bmatrix} p(X_0=1) & p(X_0=2) & \cdots & p(X_0=r) \end{bmatrix} \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1r}\\\
p_{21} & p_{22} & \cdots & p_{2r}\\\
\vdots & \vdots & \ddots &\vdots\\\
p_{r1} & p_{r2} & \cdots & p_{rr} \end{bmatrix}\\\
=& \begin{bmatrix} p(X_1=1) & p(X_1=2) & \cdots & p(X_1=r) \end{bmatrix} \end{align} $$

이걸 알면 $\pi(2)$도 간단히 쓸 수 있다.

$$ \pi(2) = \pi(1)P = \pi(0)P^2 $$

이를 일반화해서 쓰면 $$ \pi(n+1)=\pi(n)P, \quad ^\forall n=0, 1,2,…\\\
\pi(n)=\pi(0)P^n, \quad ^\forall n=0, 1,2,… $$

2) n-step transition probabilities

아까 봤던 $P$와 $p_{ij}$는 기간이 1기 넘어갈 때의 전환 확률이다. 그렇다면 다음과 같은 2단계 전환확률은 어떻게 구할까?

요것도 전사건의 법칙과 마코브 성질을 이용하면 1단계 전환확률의 곱의 합으로 나타낼 수 있다. $$ \begin{align} p_{ij}^{(2)}=p(X_2=j|X_0=i)&=\sum_{k\in S}p(X_2=j|X_1=k,X_0=i)p(X_1=k|X_0=i)\\\
&=\sum_{k\in S}p(X_2=j|X_1=k)p(X_1=k|X_0=i)\\\
&=\sum_{k\in S}p_{kj}p_{ik} \end{align} $$

자세히 보면 $p_{ij}^{(2)}$는 결국 전환행렬 $P$에서 $j$번째 열과 $i$번째 행의 내적인 것을 알 수 있다. 때문에 2단계 전환행렬 $P^{(2)}$는

$$ P^{(2)}= \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1r}\\\
p_{21} & p_{22} & \cdots & p_{2r}\\\
\vdots & \vdots & \ddots &\vdots\\\
p_{r1} & p_{r2} & \cdots & p_{rr} \end{bmatrix} \begin{bmatrix} p_{11} & p_{12} & \cdots & p_{1r}\\\
p_{21} & p_{22} & \cdots & p_{2r}\\\
\vdots & \vdots & \ddots &\vdots\\\
p_{r1} & p_{r2} & \cdots & p_{rr} \end{bmatrix}=P^2 $$

이제 이걸 n단계로 일반화해서 쓴거를 Chapman-Kolmogorov equation 이라고 한다.

Chapman-Kolmogorov Equation

$$ \begin{align} p_{ij}^{(m+n)}& = p(X_{m+n}=j|X_0=i)=\sum_{k\in S}p_{ik}^{(m)}p_{kj}^{(n)}\\\
P^{(n)}&=P^n \end{align} $$

2-3. Classification of States

마코브 체인에 대해 더 재밌는 얘기를 하려면 마코브 체인의 상태에 대한 몇 가지 정의를 짚고 넘어가야 한다.

Definition

• Accessible: 상태 $i,j$에 대해 $p_{ij}^{(n)}>0$이면 $j$는 $i$에서 accessible하며, $i \to j$라고 쓴다.

• Communicate: 상태 $i,j$에 대해 $i \to j, i\to i$이면 communicate한다고 하며, $i \leftrightarrow j$라고 쓴다.

쉽게 말하면 $i$에서 $j$로 마코브 체인을 타고 타고 타고 가다가 언젠가 한번은 들리게 되면 accessible한거고, 그 반대도 해당되면 communicate한다는 건데, 여기서 정의한 communication은 수학에서 말하는 equivalence relation에 해당한다. 뭐 별거는 아니고 그냥 communication operator인 $\leftrightarrow$에 대해 다음이 성립한다는 말이다.

1. 모든 상태는 스스로와 communicate: $i \leftrightarrow i$
2. $i \leftrightarrow j$이면 $j \leftrightarrow i$
3. $i \leftrightarrow j$, $j \leftrightarrow k$이면 $i \leftrightarrow k$

이처럼 communication이 equivalence relation이기 때문에 서로 communicate하는 상태들끼리만 모으는 식으로 마코브 체인의 상태를 각각의 communicating class로 분류할 수 있다. 무슨 말인지 예시를 통해 살펴보자. (그림 출처 https://www.probabilitycourse.com/chapter11/11_2_1_introduction.php)

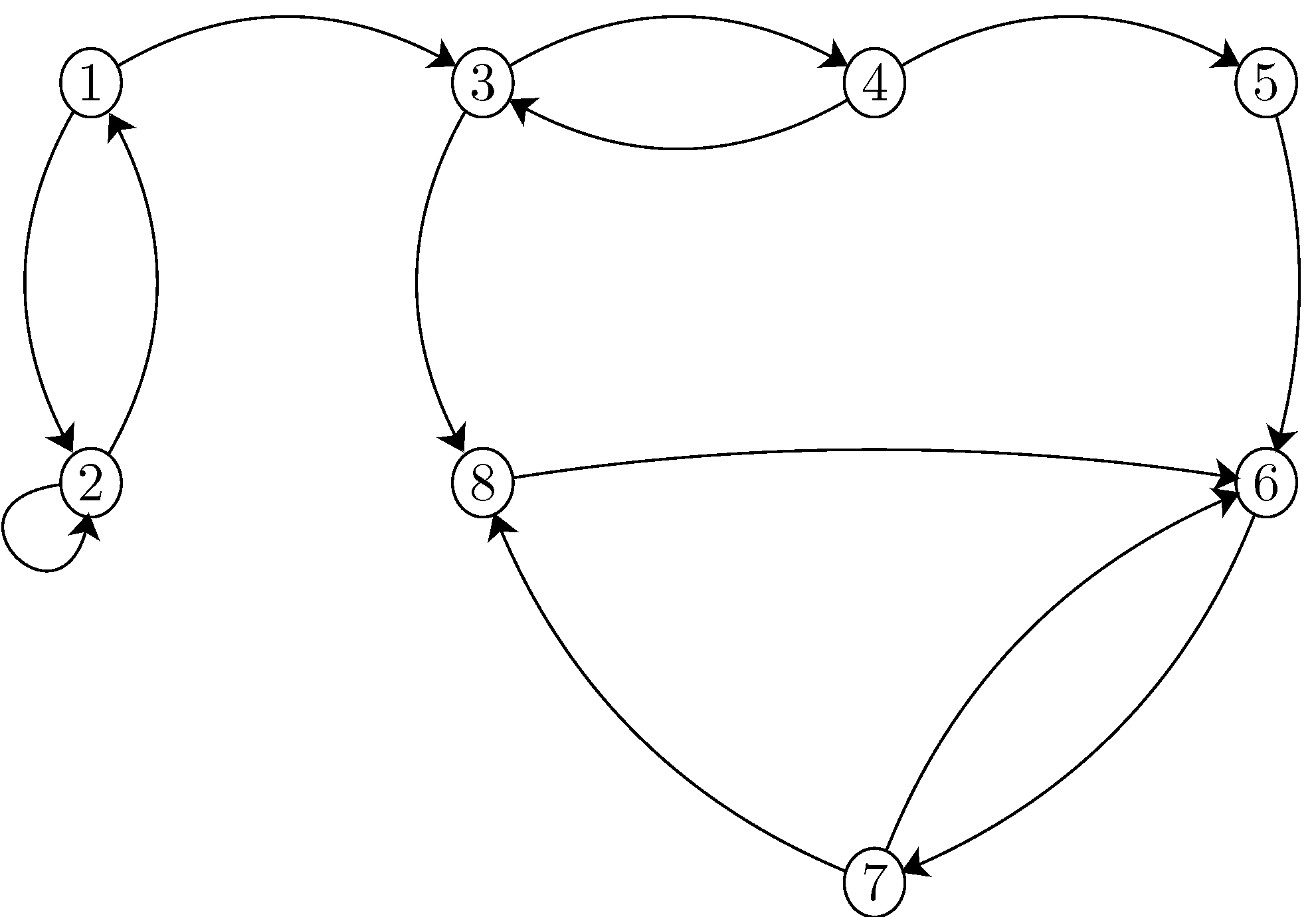
여기서 노드들을 communicating class로 나눠보자. 방법은 간단하다. 노드를 찬찬히 뜯어보면서 예컨대

“1에서 2로 가는게 있다” $\rightarrow$ “2에서 1로 언젠가 가나?” $\to$ 간다면 “1과 2는 같은 클라스^^”

라고 하면 된다. 그렇게 뜯어보면 다음과 같이 나눌 수 있다.

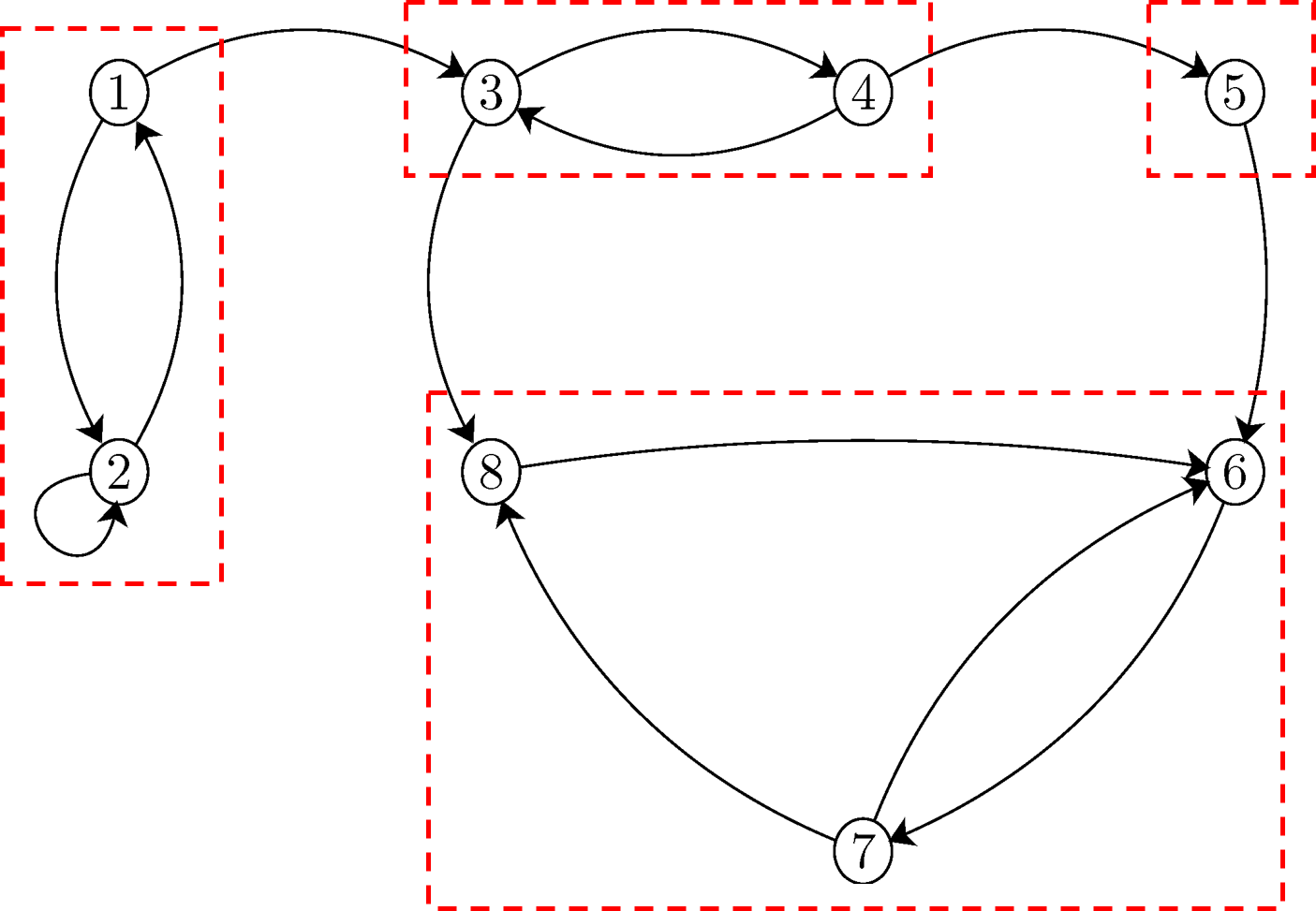
$$ \begin{align} \text{Class 1} &= {1, 2}\\\
\text{Class 2} &= {3, 4}\\\
\text{Class 3} &= {5}\\\
\text{Class 4} &= {6, 7,8} \end{align} $$

위 그림이 나타내는 마코브 체인에는 총 4가지의 communication class가 있음을 알 수 있다.

그러나 전체 마코브 체인의 모든 상태가 하나의 class에 속할 수 있다. 이런 마코브 체인을 우리는 irreducible하다고 한다.

Definition (Irreducibility) 마코브 체인의 모든 상태들이 서로 communicate하는 마코브 체인을 irreducible하다고 한다. 또 다른 정의로는

$$ ^\forall i,j \in S, ^\exists m<\infty \quad s.t.\quad p(X_{n+m}=j|X_n=i)>0 $$

왜 이름이 irreducible인지 이해해보자. 만일 위의 예시처럼 클라스가 여러 개이면, 마코브 체인이 쭉쭉 나가다가 에쿠 하고 한 클래스로 빠져버리면 영원히 그 클래스 안에 머무르게 될 수도 있다. Class 4가 그런 경우이다. 어쩌다가 한번 8이 되면, 앞으로는 영원히 6,7,8만 취할 것이다. 혹은 어떤 클라스에서 나가면, 다시는 그 클라스로 돌아올 수 없을 수도 있다. Class 1이 그런 경우이다. 이런 경우는 현재 상태에 따라 어떤 특정한 상태 $j$에 도달할 확률이 아예 없어지는 경우이며, 달리 말하면 결국 마코브 체인이 도달하는 상태가 몇 개의 class로 “reduce(환원)“될 수 있는 것이다. 만일 모든 상태가 같은 클라스에 속하면 이런 경우가 없으며, 이를 달리 말하자면

“언제 어디에 있든 언젠가는 어디로든 간다”

라고 말할 수 있는 거고, 그걸 수식으로 쓴게 irreducible의 정의이다.

이걸 한번 시뮬레이션으로도 직접 확인할 수 있다. 다음처럼 R 함수를 짜면 간단하게 이산 마코브 체인을 돌려볼 수 있다.

run.mc.sim = function(P, num.iters=50){

  num.states = nrow(P)  		 # P: transition probability
  states = numeric(num.iters)	 # placeholder vector for states
  states[1] = 1 			     # initial states
  
  for (t in 2:num.iters){
    p = P[states[t-1],] 					# transition prob at time t-1
    states[t] = which(rmultinom(1,1,p)==1)  # generate state at t
  }
  return(states)
}

이 함수를 이용해서 위에서 든 예시를 직접 생성해서 그려보면 다음과 같다.

P <- t(matrix(c( 0, 1/2, 1/2,   0,  0,   0,   0,   0,
                 1/2, 1/2, 0,   0,  0,   0,   0,   0,
                 0,   0,   0, 1/2,  0,   0,   0, 1/2,
                 0,   0, 1/2,   0, 1/2,  0,   0,   0,
                 0,   0,   0,   0,   0,  1,   0,   0,
                 0,   0,   0,   0,   0,  0,   1,   0,
                 0,   0,   0,   0,   0, 1/2,  0, 1/2,
                 0,   0,   0,   0,   0,   1,  0,   0), nrow=8, ncol=8))

set.seed(101) # reproducible
num.chains = 5
num.iterations = 100

# Generate chains
chain.states = matrix(NA, ncol=num.chains, nrow=num.iterations)
for(c in 1:num.chains){
  chain.states[,c] = run.mc.sim(P, num.iterations)
}

# Plotting
df = data.frame(step=1:num.iterations, chain.states)
colnames(df) = c('step', 'C1','C2','C3','C4','C5')
df.long = melt(df, id.vars='step', variable_name = 'chain')

ggplot(df.long, aes(x=step, y=value, group=chain, color=chain))+
  geom_line(size=1)+
  ggtitle('Reducible Markov Chain')+
  ylab('state')

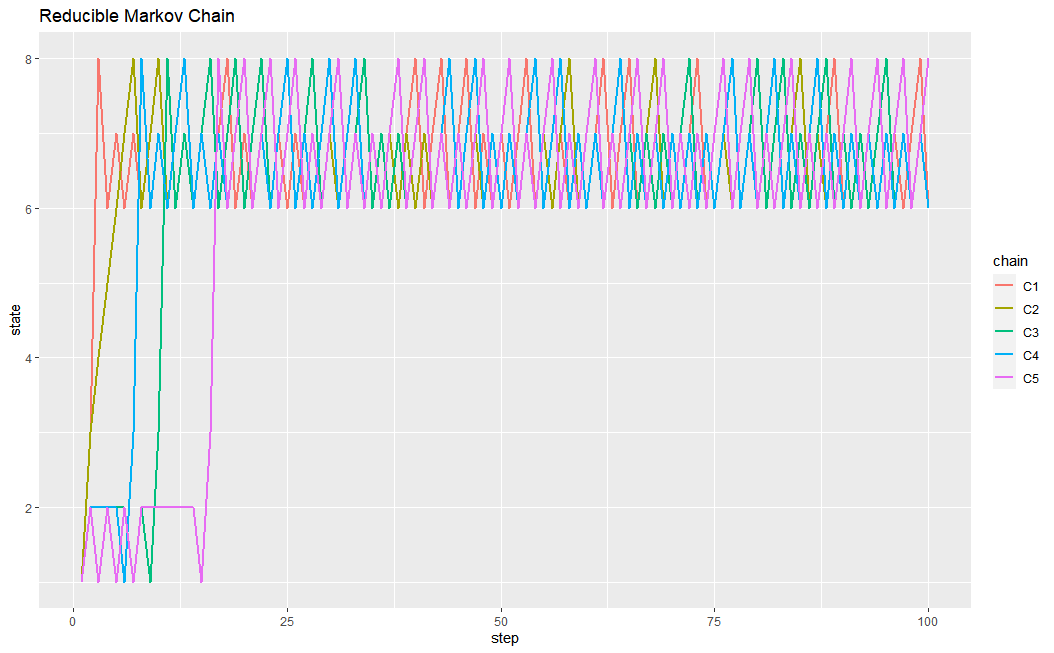
5번의 체인에서 모두 결국 6,7,8이 있는 class 4로 “reduced"된 것을 확인할 수 있다.

이 마코브 체인에서 class 4는 한번 들어오면 다시는 나갈 수 없다. 좀더 너그러이 말하자면, 한번 이 클래스에 들어오면 나중에 언젠가는 반드시 그 클래스에 또 들르게 된다. 이러한 class에 속하는 상태들을 우리는 recurrent하다고 한다. 반대로 recurrent하지 않은, 즉 한번 그 클래스에 들어왔다고 해서 나중에 그 클래스를 또 들어갈 것이라는 보장을 못하는 클래스들에 있는 상태들을 우리는 transient하다고 한다.

한 클래스에 있는 노드들은 모두 communicate하기 때문에, 한 노드가 recurrent하거나 transient하면 클래스 전체가 각각 recurrent 혹은 transient하게 된다. 또한 위의 예시에서 보듯이 마코브 체인은 transient한 클래스와 recurrent한 클래스가 같이 있을 수 있다. recurrent 와 transient의 수학적 정의는 다음과 같다.

Definition (Recurrence, Transience of states/classes):

$$ f_{ii} = p(X_{0+k}=i, \text{for some } k> 0|X_0=i) \begin{cases} =1 &\quad \text{state $i$ is recurrent}\\\
<1 &\quad \text{state $i$ is transient} \end{cases} $$

이 정의가 잘 이해가 안 되면 $1-f_{ii}$를 생각해보자. $f_{ii}$는 언젠가 한 번이라도 다시 $i$에 돌아올 확률이고, $1-f_{ii}$의 의미는 다시는 절대로 $i$로 돌아오지 않을 확률이다. recurrent하다는 것은 언젠가는 무조건 다시 돌아온다는 것이니 $1-f_{ii} =0$인 것이고, transient는 그런 보장이 없으니 $1-f_{ii} >0$인 것이다. 달리 말하자면

transient한 상태는 어떤 시점 $M(i)$이 있어 그 시점을 지나면 다시는 마코브 체인이 절대로 그 상태로 다시 돌아오지 않는다

고 생각할 수 있다.

이를 수식으로 나타내보자. $V(i)$를 마코브 체인이 $i$ 상태를 취하는 횟수라고 생각해보자. 어떤 상태 $i$에 대해 처음 마코브 체인이 $i$에서 시작했다고 하자. 그렇다면 $V(i)=k$일 확률은 다음과 같이 쓸 수 있다.

$$ p(V(i)=k|X_0=i)=f_{ii}^k(1-f_{ii}) $$

이때 $V(i)$의 기댓값은 다음과 같이 계산할 수 있다.

$$ E[V(i)|X_0=i]=\sum_{n=0}^\infty nf_{ii}^n(1-f_{ii}) = \cdots = \dfrac{1}{1-f_{ii}} $$

위 두 결과로부터 다음과 같은 결론을 내릴 수 있다.

• Transient하다는 것은 $f_{ii}<1$이라는 것이다. 때문에 $k\to \infty$에 따라 $p(V(i)=k|X_0=i)\to 0$이 될 것이다. 그러므로 어떤 수 $M(i)$가 있어 $k>M(i)$에 대해 $p(V(i)=k|X_0=i)$이 한없이 작을 것이라고 말할 수 있다. 즉 언젠가는 이 클래스를 다시는 들르지 못하게 되는 것이다.
• Recurrent한 상태에 대해서는 $E[V(i)|X_0=i]$이 무한대로 발산함을 알 수 있다. 즉 Recurrent한 상태는 마코브 체인이 무한대로 진행함에 따라 평균을 계산할 수 없을 정도로 무한히 많이 들른다는 것이다.

여기에서 자연스럽게 다름과 같은 결론을 내릴 수 있다.

• State space가 유한한 경우 적어도 하나의 클래스는 Recurrent하다. 모든 상태가 transient하다는 것은 어떤 큰 수 $M$이 있어 그 시점을 넘어가면 그 어떤 상태에도 다시 돌아가지 않는다는 것인데, 이는 모순이기 때문이다.

이렇게 해서 recurrence와 transience에 대한 이야기를 다 했다. 결론은 finite state space에 대해서는, 적어도 하나의 recurrent class가 존재하고, 마코브 체인이 무한히 지속될수록 결국 확률과정의 상태는 그 recurrent class 안에서만 머무른다는 것이다.

그렇다면 확률과정이 모든 노드를 다 지나게 하려면, 모든 노드가 하나의 recurrent한 클래스에 속해야 한다. 즉 irreducible해야 한다. 위의 예시를 irreducible하게 만들려면 어떻게 해야할까? 아래 그림처럼 각각의 클래스를 서로 이어주는 화살표를 그려, 모두 하나의 class가 되도록 하면 된다.

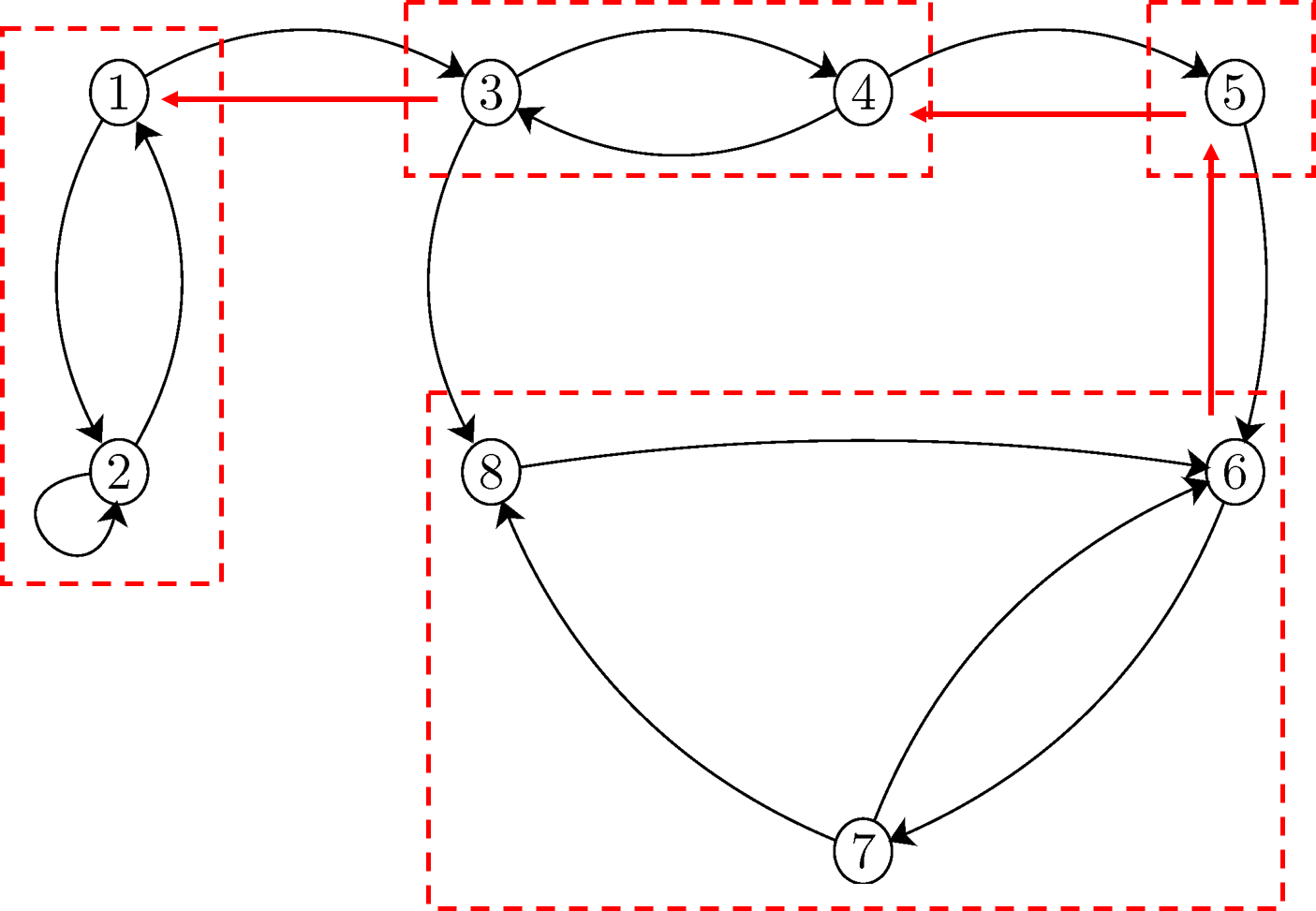
이 새로운 마코브 체인을 시뮬레이션하면 다음과 같다. 100번 넘어가는 동안 모든 상태를 골고루 누비는 것을 알 수 있다. 이런 마코브 체인을 “irreducible"하다고 한다. 위의 예시에서 상태 5는 원래 한번 6으로 넘어가면 다시는 돌아오지 못했다. 그러나 새로이 화살표를 그리면 $5 \to 6 \to 5$ 혹은 $5 \to 6 \to 7\to 8\to 6\to5$ 등의 경로를 통해 다시 5로 돌아올 수 있다. 나머지 상태들도 마찬가지이다. 때문에 Irreducible한 마코브 체인에서 모든 상태는 하나의 recurrent한 communication class에 속한 것이다.

P <- t(matrix(c( 0, 1/2, 1/2,   0,  0,   0,   0,   0,
                 1/2, 1/2, 0,   0,  0,   0,   0,   0,
                 1/3, 0,   0, 1/3,  0,   0,   0, 1/3,
                 0,   0, 1/2,   0, 1/2,  0,   0,   0,
                 0,   0,   0, 1/2,   0,1/2,   0,   0,
                 0,   0,   0,   0, 1/2,  0, 1/2,   0,
                 0,   0,   0,   0,   0, 1/2,  0, 1/2,
                 0,   0,   0,   0,   0,   1,  0,   0), nrow=8, ncol=8))


chain.states = matrix(NA, ncol=num.chains, nrow=num.iterations)
for(c in 1:num.chains){
  chain.states[,c] = run.mc.sim(P, num.iterations)
}


df = data.frame(step=1:num.iterations, chain.states)
colnames(df) = c('step', 'C1','C2','C3','C4','C5')
df.long = melt(df, id.vars='step', variable_name = 'chain')

ggplot(df.long, aes(x=step, y=value, group=chain, color=chain))+
  geom_line(size=1)+
  ggtitle('Irreducible Markov Chain')+
  ylab('state')

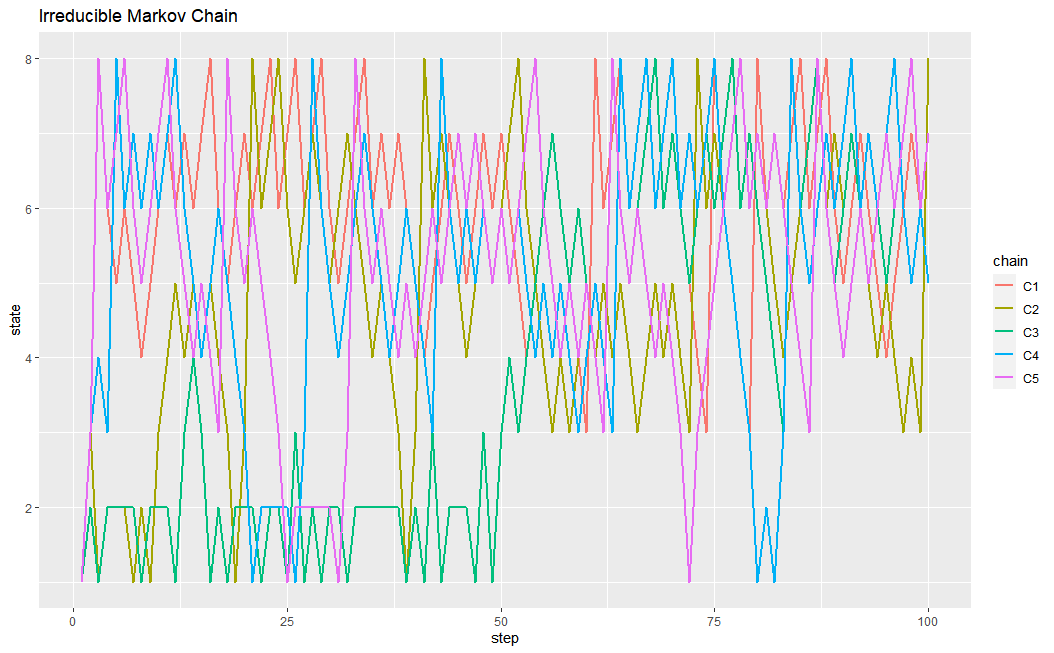
이제부터는 마코브 체인의 상태의 period에 대해 얘기해보자. 먼저 앞선 예시를 다시 가져와보자.

이때 각각의 상태에 대해서 “몇 번 화살표를 건너가야지 다시 자기 자신으로 돌아올 수 있는가"에 대해서 생각해보자. 수식으로 쓰면 우리는 각 상태에 대해 다음과 같은 숫자 $n$을 생각하고 있는 거다.

$$ n_i \text{ s.t. } p_{ii}^{(n)}> 0 $$

먼저 상태 1을 보면, 다시 자기 자신으로 돌아오려면 $1 \to 2 \to 1$ 혹은 $1 \to 2 \to 2 \to 1$의 경로를 거쳐야 한다. 즉 $n_1=3,4$이다. 마찬가지 이유로 상태 2는 $n_2=1, 2$이다. 다른 클래스를 보면 $n_8=3,5, n_7=2,3, n_6=2,3$임을 알 수 있다. 다른 상태들에 대해서도 한번 생각해보자.

그렇다면 이제는 다음과 같은 수를 생각해보자. 이때 $d(i)$를 우리는 period라고 한다.

Definition (Period of state $i$)

$$ d(i) = gcd \Big(n_i \text{ s.t. } p_{ii}^{(n)}> 0 \Big) $$

여기서 gcd는 greatest common divisor, 한국말로 최대공약수를 말한다. 어떤 상태 $i$에 대하여 $d(i)=1$이면 우리는 그 상태가 aperiodic, $1$보다 크면 periodic한다고 한다.

Definition (Periodicity)

어떤 상태 $i$에 대해 $d(i) = gcd \Big(n_i \text{ s.t. } p_{ii}^{(n)}> 0\Big )$라고 하면, 상태 $i$는

• $d(i)=1$ 이면 aperiodic 하며,
• $d(i)>1$ 이면 periodic 하다고 한다.

이게 무슨 말인지 이해하려면 $d(i)>1$의 의미를 곱씹어봐야 한다. $d(i)>1$라는 것은 결국 현재 상태가 $i$일 때 적어도 다음 상태는 $i$가 아니라는 것을 우리가 확정적으로 알 수 있다는 말이다. 이렇게 현재 상태에 따라 다음 상태가 적어도 뭐가 아닌지는 확실히 알 수 있다면 그 마코브 체인에는 어떠한 주기가 있다고 말할 수 있다. 반대로 모든 상태에 대해서 $d(i)=1$이라면, 현재 상태가 뭐든 간에 다음 상태로는 모든 경우가 다 가능한 것이고, 때문에 주기성이 없다고 하는 것이다. (이런 설명을 책이나 다른 자료에서는 찾아볼 수 없었는데, 본인이 생각하기에는 대충 이런 이유가 맞는 거 같다.)

또 중요한 성질은 바로 한 communication class 안에 있는 모든 상태는 모두 주기가 같다는 것이다. 이는 쉽게 보일 수 있다. 어떤 클래스 안에 상태 $i, j$가 있어, $i$에서 $j$로는 $n$번 화살표를 건너가 도달할 수 있고, 그 반대로는 $m$번 화살표를 건너가 도달할 수 있다고 해보자. 그렇다면 $m+n$번에 걸쳐 $i \to i$로, $j \to j$로 갈 수 있는 것이니, $m+n$의 최대공약수는 $d(i)$와 $d(j)$이다. 근데 최대공약수는 유일하지 않은가. 때문에 $d(i)=d(j)$임을 알 수 있다!

못 믿겠으면 위의 예시에서 직접 계산해보자. class 4에서 $n_8=3,5, n_7=2,3, n_6=2,3$임을 이미 봤다. 이때 3과 5의 최대공약수는 1이고, 2와 3의 최대공약수는 1이니, 모든 상태에서 period가 1임을 알 수 있다. 다른 클래스에 대해서도 직접 세보자.

지금까지는 어떤 상태가 aperiodic하다는 것의 정의를 봤다. 이제 앞서 말한 state space가 유한하고 irreducible한 (homogeneous) 마코브 체인에 대해서 생각해보자. state space가 finite하므로 적어도 어떤 클래스는 recurrent할 것이고, irreducible하므로 모든 상태가 그 recurrent한 하나의 클래스에 속해있을 것이다. 여기서 한 가지 조건만 추가하면 정말 유용한 마코브 체인이 되는데, 그 조건이 aperiodic이다. 만일 마코브 체인의 모든 상태에 대해 주기 $d(i)=1$이면, 우리는 전체 마코브 체인이 aperiodic하다고 한다.

state space가 유한하고 irreducible한 (homogeneous) 마코브 체인에 한해서, aperiodic하다는 것은 곧 transion matrix $P$가 0인 원소가 있어도 계속 곱하다보면 결국 $P^n$의 모든 원소는 0보다 크다는 것과 동치이다.

Fininte state space, homogeneous and irreducible Markov Chain is aperiodic if and only if all elements of $P^n$ are non-zero for some large $n$.

이를 엄밀히 증명하려면 정수론을 데리고 와야 하는데(http://faculty.cs.tamu.edu/klappi/csce658-s18/markov_chains.pdf), state space가 유한하고 irreducible한 (homogeneous) 마코브 체인에 한해서는 직관적으로 이해할 수 있다. $P^m$이라는 것은 $P$에 대해 그린 마코브 체인의 그림에서 화살표를 한 번에 $m$번 탈 때 $i\to j$로 갈 확률의 행렬이다. 이때 마코브 체인이 periodic하면 모든 상태에 대해 예컨대 $d(i)=2$라는 것이고, 그러면 화살표를 한 번에 하나를 타든, 두 번을 타든, 세 번을 타든 몇 번을 타든 결코 도달할 수 없는 부분이 있다는 것이다. 반대로 $d(i)=1$이라는 것은 결국 한 번에 두 개, 세 개씩 쭉쭉 타다보면 한 상태에서 다른 상태로 한 번에 도달할 수 있다는 말이다. 예시를 통해 이해해보자.

두 마코브 체인 모두 state space가 유한하고 irreducible한 (homogeneous) 마코브 체인이다. 그러나 MC (1)에서 모든 상태의 $d(i)=4$이고, MC (2)는 $d(i)=1$인 aperiodic한 마코브 체인이다. 이때 MC(1)을 보면, 화살표를 $n$번 점프했을 때 모든 상태에 도달할 수 있는 자연수 $n$은 존재하지 않는다. 1번 점프하면 1, 3, 4를 못 가고, 2번 점프하면 2, 4를 못 가고, 4번 점프하면 1밖에 못 가는 식이다. 때문에 MC (1)에서 $P^n$을 구하면 항상 0이 되는 원소가 존재한다. 그러나 MC (2)의 경우 화살표를 9번 점프하면 어떤 상태에든 도달할 수 있다(직접 확인해보자). 때문에 $P^9$를 구하면 모든 원소가 0보다 크다. 즉 9번 점프하면 어디든 갈 수 있다는 것이다. (직접 R로 계산해보자.)

이 논의를 종합해서 우리는 state space가 유한하고 homogeneous한 이산형 마코브 체인 중에서 irreducible하고 aperiodic한 마코브 체인을 다음과 같이 정의할 수 있다.

Definition (Irreducible and Aperiodic MC)

state space가 유한하고, homogeneous한 이산형 마코브 체인에 대하여,

1. 모든 상태가 하나의 communication class에 속해있으며 (irreducible), (혹은 $^\forall i,j \in S, \;^\exists m<\infty \quad s.t.\quad p(X_{n+m}=j|X_n=i)>0$)
2. 모든 상태의 주기가 $d(i)=1$이면 (aperiodic), (혹은 $^\exists n \quad s.t.\quad p_{ij}^{(n)} > 0 \quad ^\forall i,j\in S$ )

이러한 마코브 체인을 Irreducible이고 Aperiodic하다고 한다. 또한 state space가 유한할 때는 이 두 조건만 만족하면 Ergodic 마코브 체인이라고 한다.

지금까지 큰 공을 들여서 irreducible하고 aperiodic한 마코브 체인을 설명한 이유는, 이 마코브 체인이 굉장히 유용한 성질을 가지고 있기 때문이다. 이제부터 살펴보겠다.

2-4. Stationary and Limiting Distributions

이 부분이 아마 마코브 체인에서 가장 어려운 부분일 것이다. 이 부분에서는 증명이나 간략한 직관을 소개하지 않고 여러 정리를 제시한다. 때문에 더 알고싶은 부분은 말미의 참고 문헌에 있는 사이트를 보면 되겠다. 본인은 아마 학교 수업을 들어야 이해를 할 것 같다…

이제 우리의 관심은 마코브 체인의 “long-term behavior"이다. 즉 $n\to \infty$일때 finite한 state space에서의 분포에 관심이 있는 것이다.

$$ \pi^{(n)} = \begin{bmatrix} p(X_n=0)&p(X_n=1)&\cdots&p(X_n=r) \end{bmatrix} $$

이러한 분포를 우리는 마코브 체인의 Limiting distribution이라고 한다. 엄밀히 정의하면 다음과 같다.

Definiton (Limiting Distribution)

다음의 조건을 만족하는 분포 $\pi= \begin{bmatrix} \pi_0& \pi_1&\cdots&\pi_r \end{bmatrix}$을 limiting distribution이라고 한다.

1. $\pi_j = \lim_{n\to \infty}p(X_n=j|X_0=i) \quad ^{\forall}i,j\in S$
2. $\sum_{j\in S}\pi_j =1$

Limiting distribution을 어떻게 찾을 것인가?

그렇다면 state space가 유한하고 homogeneous한 이산형 마코브 체인에서 이러한 극한 분포를 어떻게 찾을 수 있을까? 일단 다음의 사항을 고려하자.

1. state space가 유한하다는 것은 적어도 하나의 recurrent한 class를 가지고 있다는 말이다.
2. 이때 마코브 체인이 irreducible하다면 모든 상태가 하나의 recurrent한 class에 속해 있다는 말이다. 즉 모든 상태에 언젠가 한 번씩은 꼭 들른다.
3. 이때 마코브 체인이 aperiodic하다면 어떤 상태에서도 아무 상태에나 갈 수 있다는 말이다. 즉 현재 $i$에 있으면 다음에는 절대 $j$로 못 가는 그런 일은 없다.

직관적으로 생각해보면, 마코브 체인이 이러한 조건을 만족한다면, 마코브 체인을 계속 실행했을 때 마코브 체인이 한 상태에 있을 장기 빈도 $1/V_n(i)$ $(n\to \infty)$가 그 상태의 극한 확률 $\pi_i$에 수렴할 것으로 생각할 수 있다. 때문에 극한 분포를 찾고 싶다면 그냥 마코브 체인을 계속 실행시켜서 장기 빈도를 구하면 된다.

정확히 말하면, 유한한 state space에서는 마코브 체인이 irreducible하기만 하면 모든 상태가 하나의 recurrent class에 속하기 때문에, 극한분포는 다음과 같이 유일하게 존재함을 보일 수 있다.

$$ \lim_{n\to\infty}\dfrac{V_n(i)}{n}= \pi_i \quad ^\forall i\in S $$

다만 여기에서 마코브 체인이 aperiodic하기까지 한다면, 이 극한분포는 다음과 같이 구할 수 있다.

$$ \lim_{n\to\infty} p_{ji}^n= \lim_{n\to\infty} p(X_n=i|X_0=j) =\pi_i \quad ^\forall i,j\in S $$

이걸을 전환행렬 $P$를 이용하여 표현하면 다음과 같이 쓸 수 있다.

$$ \pi = \lim_{n\to\infty}\pi(n) = \lim_{n\to\infty}[\pi(0)P^n] \quad \text{for any $\pi(0)$} $$

즉 극한 분포 $\pi$를 찾으려면 그냥 $P$ 행렬을 무진장 많이 곱하면 된다. 그러나 이게 말처럼 쉬운 일은 아니기 때문에, 우리는 한 가지 트릭을 이용하여 극한분포를 구하는 방정식을 찾을 수 있다.

그러면 먼저 stationary distribution의 정의를 알아야 한다.

Definiton (Stationary Distribution)

다음의 조건을 만족하는 분포 $\pi= \begin{bmatrix} \pi_0& \pi_1&\cdots&\pi_r \end{bmatrix}$을 $P$가 정의하는 마코브 체인의 stationary distribution이라고 한다.

1. $\pi P =\pi$
2. $\sum_{j\in S}\pi_j =1$

finite state space에서 stationary 분포는 유일하지 않을 수 있다. 예컨대 recurrent class가 여러 개 있다면, 여러 recurrent class 중에 어느 곳에 빠지게 되냐에 따라 stationary distribution이 다를 것이다. 그러나 만일 마코브 체인이 irreducible하면 stationary 분포는 유일하게 존재한다.

이제 다음과 같은 논리에 따라 극한분포를 구하는 방정식을 유도해보자. finite state space에 irreducible하고 aperiodic한 마코브 체인에 대해서는

1. 극한분포가 유일하게 존재하며, 그게 곧 stationary 분포이다. (하나의 분포로 수렴하니까)
2. stationary 분포도 유일하게 존재한다.
3. 때문에 stationary 분포를 구하면 그것이 바로 극한분포이다!

부연설명

finite state space이며 irreducible하면 마코브 체인을 무한히 돌리며 기록한, 어떤 상태에 체류하는 장기 빈도가 stationary 분포라고 할 수 있는데, 여기닥가 aperiodic하기까지 하다면 장기빈도를 기록할 필요도 없이 $\lim_{n\to \infty}\pi P^n$가 극한분포 자체로 수렴한다고 얘기할 수 있다. 참조: stochastic-I-MCII.pdf (columbia.edu)

즉 우리는 transition matrix $P$를 무진장 곱하지 않고도 위의 방정식 $\pi P =\pi$을 만족하는 $\pi$만 구하면, 그게 극한 분포라고 확신할 수 있는 것이다. (누누이 말하지만 이게 가능한 이유는 우리가 finite state space에 irreducible하고 aperiodic한 마코브 체인에 대해서만 말하고 있기 때문이다!)

이제 우리는 극한분포를 구하기 위해서는 다음의 $r$개의 방정식을 풀면 된다.

$$ \begin{align} \pi_j &= \sum_{k\in S}\pi_k p_{kj} \quad ^\forall j\in S={1,2,…,r}\\\
\sum_{j\in S}\pi_j&=1 \end{align} $$

근데 참… 이것도 말은 쉽지 이걸 다 푸는게 또 일이다. 그래서 또 간단한 트릭을 사용한다. 일단 다짜고짜 다음의 정의를 생각해보자.

Definition (Reversibility)

마코브 체인 $\{X_n, n=0, 1, 2,…\}$이 stationary distribution $\pi$를 가진다고 하자. 이때 다음의 방정식을 detailed balance equation이라고 하며, 이를 만족하는 마코브 체인을 $\pi$에 대하여 reversible하다고 한다.

$$ \pi_i p_{ij} = \pi_jp_{ji} \quad ^\forall i,j\in S $$

무슨 뜻일까?

• 처음 초기 분포가 $\pi(0)=\pi$대로 되어있다고 하자. 그러면 $\pi_i p_{ij}$는$i$에서 $j$로 흐르는 확률의 양을, $\pi_jp_{ji}$는 $j$에서 $i$로 흐르는 확률의 양을 의미한다.

  Detailed balance란 모든 노드에서 흘러들어오는 확률의 양과 흘러나가는 확률의 양이 같다는 이야기이다.

  이 때문에 이걸 만족하는 마코브 체인을 Reversible하다고 하는 것이다.

• 이는 $\pi P =\pi$보다 훨씬 더 빡센 조건이다. 당장 방정식의 개수만 봐도 그렇다. $\pi P =\pi$은 $r$개의 방정식으로 이뤄져 있다. 그러나 위의 Detailed Balance 방정식은 $S$의 모든 $i,j$ 쌍에 대해 모두 성립해야 하니 대충 봐도 ${r \choose 2}=\frac{r(r-1)}{2}$개의 방정식이 나온다. 때문에 Stationary 분포가 존재하는 마코브 체인에서 위의 detailed balance equation의 해가 존재하면 그게 바로 stationary distribution임을 알 수 있다. 직접 보이려면, 수식으로 보이면 양 변을 일단 $i$에 대해 합쳐보면 된다. 그러면 $\pi P = \pi$를 만족함을 알 수 있다.

  $$ \sum_i \pi_i p_{ij} = \sum_i \pi_jp_{ji} = \pi_j \sum_i p_{ji}= \pi_j $$

• 직관적으로 이해하자면 다음과 같다. 설명은 여기서 참조하였다. (https://cims.nyu.edu/~holmes/teaching/asa19/handout_Lecture3_2019.pdf) 화살표로 이어진 마코브 체인에서 각 노드를 서울시의 구, 화살표를 각 구를 잇는 도로라고 생각해보자. (irreducible 하므로 모든 구가 적어도 하나의 다른 구와 왕복 도로로 연결되어 있다.) stationary 분포가 존재할 조건은 global balance라고도 하는데, 이는 차들이 쌩썡 지나다니다 보면 어느 순간부터는 모든 시점에서 각 지역구에 있는 차들의 수가 변하지 않는다는 의미이다. 여기에다가 detailed balance까지하려면, 두 지역구를 잇는 모든 도로에서 들어오는 차의 수와 나가는 차의 수가 같다는 거다. 그림으로 이해해보자. 아래 두 경우 모두 서대문구를 지나는 차의 수는 일정하다. 그러나 오른쪽의 그림에는 서대문구를 지나는 차의 수도 일정하고, 종로구와 마포구에 난 도로를 진입하고 진출하는 차의 수까지 일정하다. 그러니 Detailed balance가 더 강력한 조건이다!

  

극한분포 구하는데 2 (global balance)에서 3(detailed balance)으로 가면 식이 더 많아지니 굳이 이런 수고를 해야 하나 싶을 것이다. 그러나 우리가 공을 들여서 3을 말한 데에는 이유가 있다. MCMC를 하기 위해서이다.

3. MCMC: Intuition

지금까지 우리는 어떤 마코브 체인에서 $P$를 알 때 극한분포 $\pi$를 어떻게 구할 수 있는지 알아봤으며, 지난 섹션에서 결국 detailed balance 방정식의 해가 바로 $\pi$인 것을 배웠다. 근데 이걸 반대로 생각할 수 있다. 어떤 분포 $\pi$를 극한분포로 가지는 마코브 체인을 어떻게 만들 수 있을까? 마코브 체인을 만든다는 것은 곧 전환행렬 $P$를 만든다는 것이다. $\pi$를 알 때 어떻게 $P$를 만들어야 하는가!

일단 $\pi$가 이산형이고 유한한 공간에서 정의된 확률분포라는 가정이 있어야 한다. 그래야 위에서 말한 finite space 마코브 체인의 성질을 이용할 수 있으니까. 서두에서 말했지만 어차피 64비트 컴퓨터로 시뮬레이션을 하기 때문에 크게 무리가 있는 가정은 아니다. 이제 우리는 마코브 체인이 irreducible하고 aperiodic하며, 극한분포가 $\pi$가 되도록 전환행렬 $P$를 만들어야 한다.

그럼 앞서 논의한 1, 2, 3을 거꾸로 타고 올라갈 수 있다. 일단 내가 원하는 분포 $\pi$에 대해서 다짜고짜 detailed balance equation의 해가 되도록 $p_{ij}$를 만들자. 그러면 이 $p_{ij}$는 $\pi$에 대해 Reversible한 마코브 체인을 정의하며, $\pi$는 이 마코브 체인의 stationary 분포라는 것을 알 수 있다. 그렇다면 이제 남은 것은 이 마코브 체인이 실제로 ergodic함을 보이는 것이다.

요컨대, 어떤 분포 $\pi$를 유일한 극한분포로 하는 마코브 체인을 만들기 위해서는, 전환행렬 $P$가 다음의 조건을 만족해야 한다.

1. $P$가 정의하는 마코브 체인은 ergodic(irreducible and aperiodic)하다. 즉 state space를 골고루 잘 돌아다닌다.
2. $P$가 정의하는 마코브 체인의 극한분포는 $\pi$이어야 한다.

2의 조건은 $\pi$에 대하여 detailed balance 방정식을 풀면 “충분히” 만족할 수 있다. 문제는 1인데, 우리는 detailed balance의 해인 $P$가 ergodic함을 보여야 한다. 증명은 보이지 않겠으나, 만일 모든 상태에 대하여 $p_{ij}$와 $\pi_i$ 모두 양수라면, $\pi$를 stationary 분포로 가지는, $P$로 정의된 마코브 체인은 ergodic함이 알려져 있다. 자세히 쓰자면,

(Leo Breiman. The strong law of large numbers for a class of markov chains. The Annals of Mathematical Statistics, 31(3):801–803, 1960)

Fundamental Theorem

If a homogenous Markov chain on a finite state space with transition probabilities $T(x, x')$ has $\pi$ as an invariant distribution and

$$ v = \min_{x}\min_{x':\pi(x')>0} T(x, x')/\pi(x') >0 $$

then the Markov chain is erogic, i.e., regardless of the initiai probabilities $p_0(x)$,

$$ \lim_{n \to \infty} p_n(x) = \pi(x) $$

실제로 마코브 체인을 사용하여 상수배를 모르는 어떤 확률분포 $p(x)$에서 샘플링을 할 때, state space안에서 pdf는 왠만하면 0보다 클 것이고, 전환확률도 0보다 크도록 만들면, 위의 조건은 큰 문제없이 지켜질 것이다.때문에 MCMC 알고리즘을 만들때 가장 중요한 것은

목표 확률분포 $p(x)$에 대하여 detailed balance를 만족하는 전환확률 $p_{ij}$

를 만드는 것이며, 이를 어떻게 만드느냐에 따라 MCMC의 방법들이 갈린다.

References

여기저기서 많이 참조했는데 뭐이가 어드레서 왔는지는 잘 모르겠는데 적어보자면

1. Hoff, P. D. (2009). A first course in Bayesian statistical methods. New York: Springer.

2. Kruschke, J. K. (2015). Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Burlington, MA: Academic Press.

3. Ross, S. M. (2013). Simulation. San Diego: Academic Press.

4. Leo Breiman. The strong law of large numbers for a class of markov chains. The Annals of Mathematical Statistics, 31(3):801–803, 1960

5. http://faculty.cs.tamu.edu/klappi/csce658-s18/markov_chains.pdf (마코브 체인 필요한 내용만 간략히 훑겠다 하면 좋음)

6. https://www.probabilitycourse.com/chapter11/11_2_1_introduction.php (마코브 체인 필요한 내용만 간략히 훑겠다 하면 좋음)

7. https://www.math.ucdavis.edu/~gravner/MAT135B/materials/ch15.pdf (좀 더 깊게 파고 들고 싶다)

8. http://www.columbia.edu/~ks20/stochastic-I/stochastic-I-MCII.pdf (좀 더 깊게 파고 들고 싶다)

9. http://www.robots.ox.ac.uk/~fwood/teaching/C19_hilary_2015_2016/mcmc.pdf (MCMC와 연관해서 보는 마코브 체인, 깔끔한데 설명이 부족함)

10. https://cims.nyu.edu/~holmes/teaching/asa19/handout_Lecture3_2019.pdf (MCMC와 연관해서 보는 마코브 체인, 이게 설명이 잘 되어있다)