(MCMC) 베이지안 사후분포 근사를 위한 MCMC 방법론

0. 개요

베이지안에서 모수에 대한 추론은 곧 모수의 분포를 구하는 것이다. 미지의 수에 대한 불확실성을 확률로 표현하였으니, 베이즈 정리를 이용해 데이터의 불확실성과 거짓말처럼 깔끔하게 같이 섞을 수 있기 때문이다. 그러나 아쉽게도 그 결과로 나오는 분포는 항상 깔끔하지만은 않다. 물론 데이터에 대한 모델을 지수분포족으로 한정하고, 그에 대응하는 또다른 특별한 지수분포족 분포함수를 사용하면, 사후분포의 모수를 쉽게 구할 수 있는데, 이러한 경우를 Prior-Posterior 간에 Conjugacy가 있다고 한다. 그러나 많은 경우 복잡한 데이터에 맞게 모델을 만들다 보면 해석적이지 않은 사후분포에 맞닥뜨리게 된다. 손으로는 구할 수 없는 것이다. 이때 몬테카를로 시뮬레이션을 통하여 사후분포를 근사할 수 있는데, 이번 보고서에서는 그 방법에 대해 알아보도록 한다.

1. 문제의 실체

우리가 맞닥뜨린 문제를 해결하기 전에 먼저 문제의 성격에 대해 탐구하자. 베이즈 추론의 알파이자 오메가인 베이즈 정리를 활용한 베이즈 추론은 다음과 같이 이뤄진다.

$$ \begin{align*} \text{Likelihood}\quad& p(D|\theta)\\\
\text{Prior Belief}\quad& p(\theta)\\\
(Evidence \quad& p(D) = \int p(D|\theta)p(\theta) d\theta\;)\\\
\text{Updated Belief} \quad &p(\theta|D) = \dfrac{p(D|\theta)p(\theta)}{p(D)} \end{align*} $$

베이지안 데이터 분석의 필수 요소는 딱 두 가지이다. 먼저 데이터에 대하여 Likelihood 모델을 세우고 (Model Specification), 그 다음 모델의 모수에 대한 불확실성을 확률분포로 특정한다 (Prior Specification). 그렇게 하면 베이즈 정리를 통해 사후분포가 완전히 특정이 되며, 베이즈 추론은 끝난다. 다만 문제는 특정이 된 사후분포의 형태인데, 분모에 있는 Evidence를 구하기 위해서는 데이터의 모델을 모델의 모수에 대한 사전 가중치로 적분해야 하지만, prior-posterior conjucay가 없을 경우 대개 적분이 불가능하다. 때문에 우리는 그 형태를 수치적인 방법으로 근사를 해야한다.

분포를 근사하는 가장 직관적인 방법은 그 분포를 따르는 샘플을 무수히 많이 생성하여, 그 샘플이 이루는 경험분포를 보는 것이다. 이때 우리가 근사하는 사후분포는 분모인 Evidence를 모르기 때문에 정확한 식은 모르지만, Likelihood와 Prior Belief의 곱에 비례하는 것만큼은 안다. 즉 우리는 확률분포를 어떤 상수배까지 알고 있을 때("upto a multiplicative constant") 이 분포를 따르는 샘플을 생성해야 하는 것이다. 이를 어떻게 해결할 수 있을까?

1-1. Grid Approximation

가장 단순한 방법은 일단 모든 가능한 경우의 수에 대하여 Likelihood와 Prior Belief의 곱을 구하는 것이다. 즉 연속형인 모수 공간을 마치 Grid처럼 촘촘한 이산형으로 나누고, 모든 모수의 조합에 대해 Likelihood와 Prior Belief의 곱을 계산하는 것이다. 이를 수식으로 나타내면 다음과 같다. 편의를 위해 모수가 2개인 정규분포 Likelihood를 가정해보자. 여기서 세타는 평균을, 틸다 시그마 제곱은 분산의 역수인 precision을 나타낸다.

다음과 같이 데이터의 분포를 정규분포로 모델링하고, 정규분포의 평균에 대한 믿음을 정규분포로, precision에 대한 미음을 감마분포로 준다고 하자.

$$ \begin{align} \text{Model Specification:}&\quad D \sim N(\theta, \tilde\sigma^2)\\\
\text{Prior Specication:}&\quad \tilde\sigma^2 \sim \Gamma(\nu_0/2, \nu_0\sigma_0^2/2)\\\
&\quad \theta \sim N(\mu_0, \tau_0^2) \end{align} $$

이때 Grid Approximation은 사후분포를 다음과 같이 근사한다.

$$ \begin{align} p(\theta_i, \tilde\sigma_j^2|D) &= \dfrac{p(\theta_i, \tilde\sigma_j^2,D)}{\sum_{g=1}^G\sum_{h=1}^H p(\theta_g, \tilde\sigma_h^2,D)}\\\
(p(\theta_i, \tilde\sigma_j^2,D) &= dnorm(\theta_i, \mu_0, \tau_0^2)\times dgamma(\tilde\sigma^2_j, \nu_0/2, \nu_0\sigma_0^2/2)\times \prod_{k=1}^N dnorm(x_k, \theta_i, \tilde\sigma^2_j)) \end{align} $$

즉 평균이 가질 수 있는 값들 G개와, Precision이 가질 수 있는 값들 H개에 대해 함수값을 모두 계산하고 각각의 값을 전체의 합으로 나누는 것이다. 이 방법은 특별한 지식 없이 단순히 함수값을 계산하는 것만으로도 분포를 근사할 수 있다는 장점이 있지만, 모수의 개수가 늘어날수록 계산해야하는 값도 많아지는 치명적인 단점, 즉 Curse of Dimenionality에서 자유롭지 않다. 때문에 다른 방법이 필요하다.

2. Markov Chain Monte Carlo Methods

앞서 살펴본 Grid Approximation에서는 모수가 가질 수 있는 모든 값에 대하여 Likelihood x Prior의 값을 구하였다. 그러나 굳이 모든 값에 대하여 계산을 할 필요가 없이, 가능한 모든 값 중에 아무 지점이나 “출발점"으로 정하고, 그 초기값에서 어떤 메커니즘에 의해 다른 지점으로 “이동"하는 과정을 반복해보자. 이때 자리를 이동하는 그 메커니즘이 뒤이어 말할 어떤 조건들을 만족하면, 지나온 자리들을 마치 어떤 분포에서 형성된 샘플처럼 간주할 수가 있다. 이것이 바로 MCMC 샘플링의 요체이다.

MCMC를 직관적으로 이해하는 가장 좋은 방법은 등고선을 예시로 드는 것이다. 산을 상상해보자. 확률분포의 정확한 식을 안다는 것은 산의 모든 지점에서의 정확한 해발고도를 안다는 것이다. 그러나 확률분포를 어떤 상수배까지 아는 것은, 모든 지점에서의 정확한 해발고도를 알 수는 없지만, 지금 서있는 지점이 주위에 비해 높고 낮은지는 알고 있다는 것이다. 우리는 지도 없이, 마치 게임 스타크래프트에서 시야가 1인 유닛처럼, 전후와 좌우의 높이만 알고 있으며, 우리의 목적은 최대한 산의 개략적인 모습을 등고선으로 그리는 것이다. 산의 개형을 잘 파악하려면 어느 한 곳에 머물지 않고 산의 구석구석을 누벼야 하며, 그 중에서도 특히 높은 곳을 위주로 가야할 것이다. 이러한 “스캔"을 가능하게 해주는 방법이 바로 MCMC이다.

이처럼 MCMC 방법의 핵심은 산의 한 지점에서 다른 지점으로 이동하는 메커니즘이고, 이 메커니즘을 어떻게 하냐에 따라 MCMC에는 대표적인 두 가지 방법 Metropolis-Hastings 알고리즘과 Gibbs Sampler 알고리즘이 있다. 그 전에 먼저 Markov Chain에 대해 간략히 이해하는 것이 중요하다. 어떤 확률변수가 Markov Chain을 따를 때, 어떻게 하여 그 확률변수의 분포를 근사할 수 있는지 공부해보자.

2-1. 마코브 체인이란?

이 부분은 이전 자료 “Discrete-Time Markov Chain with Finite State Space for MCMC"으로 대체한다. 핵심은 타겟 분포 $p(x)$에 대해서 다음의 detailed balance equation을 만족하는 transiton operator $T(x, x')$을 찾는 것이다.

$$ p(x)T(x, x') = p(x')T(x',x) \quad ^\forall x, x'\in S\\\
\text{equivalently,}\quad\pi_i p_{ij} = \pi_j p_{ji} \quad ^\forall i,j\in S $$

2-2. Metropolis-Hastings Algorithm

우리가 하고자 하는 바는 다음과 같다. 어떤 분포 f를 따르는 확률변수 X에 대해, 그 pdf에서 어떤 상수 C를 계산하기가 굉장히 곤란하다고 해보자.

$$ X \sim f(X=j) = C\times b(j) $$

먼저 다음과 같이 Proposal Distribution을 만든다. (우리는 지금 state space가 finite하다고 가정했음을 상기하자.)

$$ \begin{align} \text{Proposal probability matrix} \quad Q_{N,N} &= \begin{pmatrix} q_{1,1} & q_{1,2} & \cdots & q_{1,N}\\\
q_{2,1} & q_{2,2} & \cdots & q_{2,N}\\\
\vdots & \vdots & \ddots &\vdots\\\
q_{N,1} & q_{N,2} & \cdots & q_{N,N}\
\end{pmatrix} \\\
\\\
\text{Proposal proability}\quad q_{i,j}& = p(X_t=j|X_{t-1}=i) \end{align} $$

예컨대 임의의 초기치로 주어진 현재 상태가 $i$라고 해보자. 이때 위의 proposal probability에 따라 다른 sample 다음 상태 $j$를 추출하는 것이다. 하지만 여기서 끝이 아니다. 우리의 목적은 $\pi_i p_{ij} = \pi_j p_{ji}$를 만족하는 transition probability를 만드는 것이며, 이를 위해서는 하나의 조건이 더 필요하다. 예컨대 생성된 다음 상태가 $j$일때, $\alpha_{i,j}$의 확률로 그 상태를 받아들인다고 하자. 즉 일종의 Accecpt Probability를 인위적으로 만드는 것이다. 이렇게 해서 만들어진 transiton probability를 쓰면 다음과 같다.

$$ \begin{align} \text{Transition probability} & \quad p_{i,j} = q_{i,j}\alpha_{i,j}\\\
& \quad p_{i,i}=q_{i,i}\alpha_{i,i} + \sum_{k\neq i}q_{i,k}(1-\alpha_{i,k}) \end{align} $$

이때 이 transition proability가 irreducible하고 aperiodic한 조건을 만족하려면 $\alpha_{i,j}$는 다음과 같이 정해진다.

$$ \begin{align} &\pi_i p_{i,j} = \pi_j p_{j,i} \quad \Leftrightarrow \quad \pi_i q_{i,j}\alpha_{i,j} = \pi_j q_{j,i}\alpha_{j,i}\\\
\text{Let}\quad&\alpha_{i,j} = \min(\dfrac{\pi_j q_{j,i}}{\pi_i q_{i,j}},1) = \min(\dfrac{b(j) q_{j,i}}{b(i) q_{i,j}},1)= \min(\dfrac{b(j)}{b(i)},1),\\\
\text{then}\quad&\pi_i q_{i,j}\min(\dfrac{\pi_j q_{j,i}}{\pi_i q_{i,j}},1) = \pi_j q_{j,i}\min(\dfrac{\pi_i q_{i,j}}{\pi_j q_{j,i}},1) \quad ^\forall i,j\in S \end{align} $$

이게 무슨 의미일까? 수식으로 살펴보면 다음과 같다. 위 식에서 $\pi_j$는 곧 우리가 모르는 분포, 미지의 분포에서 상태 $j$의 확률이다. 지금 우리가 한 것은 인위적으로 proposal 확률을 만들고, 전환확률이 detailed balance 조건을 만족하도록 accept 확률을 위와 같이 정하였기 때문에, (이전 자료에서 말한 몇 가지 가정을 만족한다고 하면) transition 확률을 이처럼 정의한 마코브 체인의 극한분포는 실제 미지의 분포 $\pi_j$에 수렴할 것임을 알고 있다.

(부연설명을 하자면, 만일 $Q$가 대칭행렬이라면, $q_{ij}=q_{ji}$이므로, 그냥 사라진다. 실제로는 proposal 분포를 노말분포로 할 것인데, 노말분포에서도 마찬가지로 어느 두 지점에서 대해서도 $q_{ij}=q_{ji}$가 성립함을 조금만 생각해보면 알 수 있다.)

좀 더 직관적으로 설명하자면, 모수 공간의 어떤 지점 $i$ 에서 임의로 (proposal $q_{i,j}$에 의하여) 다른 지점 $j$ 으로 간 것이다. 이 때 $j$ 지점에서의 “높이” (상수를 모르는 pdf의 값)가, 이전 지점 $i$ 지점에서의 높이보다 높으면 묻지도 따지지도 않고 그냥 $j$ 지점으로 옮겨가지만, 만일 높이가 더 낮다면 그 높이에 비례하는 확률만큼 그 지점으로 이동하는 것이다. 예컨대 새로운 지점에서의 높이가 절반이라면, 동전을 던져 앞면이 나오면 가고 뒷면이 나오면 가지 않는 식이다! 놀랍게도 이런식으로 계속 이동을 하면 마치 원래 미지의 분포에서 추출한 것만 같은 샘플을 추출할 수 있는 것이다!

한번 예시를 들어보자. Grid Approximation에서 든 예시와 같은 상황을 가져와보자.

$$ \begin{align} \text{Likelihood}&\quad D \sim N(\theta, \tilde\sigma^2)\\\
\text{Prior}&\quad \tilde\sigma^2 \sim \Gamma(\nu_0/2, \nu_0\sigma_0^2/2)\\\
&\quad \theta \sim N(\mu_0, \tau_0^2)\\\
\text{Psterior} &\quad p(\theta_i, \tilde\sigma_j^2|D) \propto p(\theta_i, \tilde\sigma_j^2)\times p(D|\theta_i, \tilde\sigma_j^2)\\\
&= dnorm(\theta_i, \mu_0, \tau_0^2)\times dgamma(\tilde\sigma^2_j, \nu_0/2, \nu_0\sigma_0^2/2)\times \prod_{k=1}^N dnorm(x_k, \theta_i, \tilde\sigma^2_j) \end{align} $$

이때 모수 평균과 precision이 이루는 모수공간에서 임의의 점을 초기 시작점으로 삼고, 주변의 임의의 점을 탐색할 proposal 분포를 임의로 설정한 다음에, 두 지점에서의 Likelihood x Prior 값을 비교하여 MH 샘플링을 진행한다.

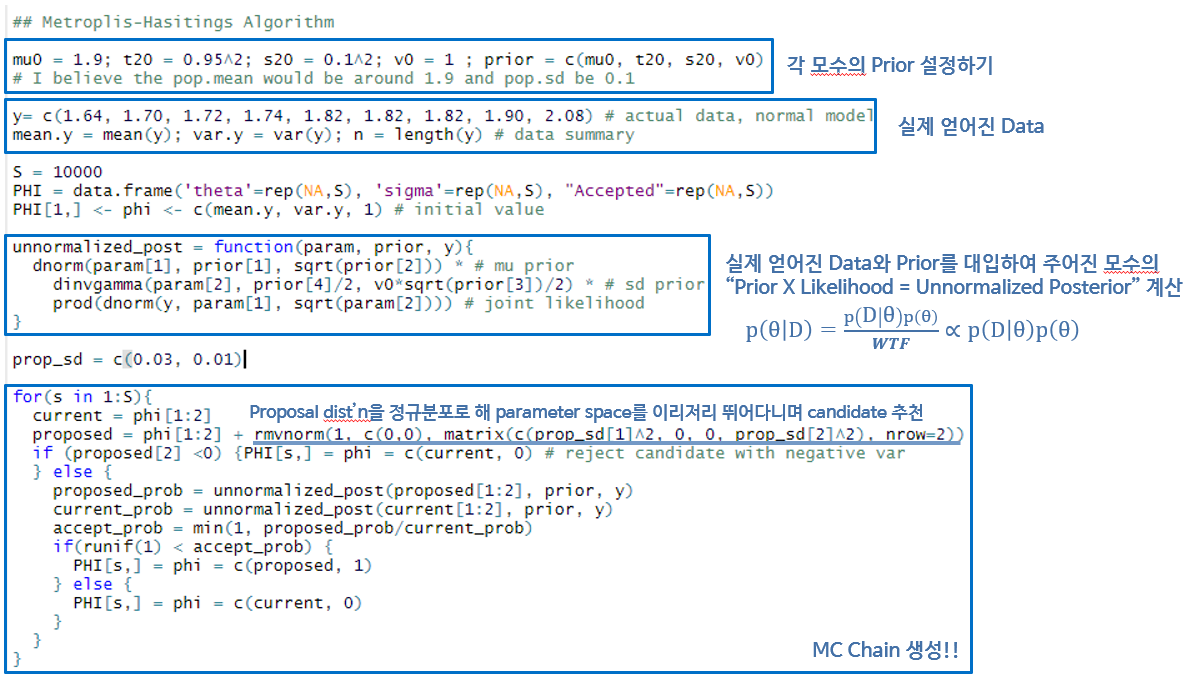
먼저 임의로 어떤 데이터를 가져오고, 그 데이터의 분포에 대한 prior의 모수를 설정한다. 그 다음 현재 지점과 제안된 지점에서의 높이를 비교할 함수 unnormalized_post를 정의하고, 한 지점에서 다른 지점을 제안할 proposal 분포를 정규분포로 정의한다. 정규분포를 선택한 이유는 별다른 것은 아니고 그냥 전후좌우 차별없이 제안을 하기 위함이며, 분산이 0보다 작은 경우는 인위적으로 제거한다. 이때 proposal 분포의 분산을 어떻게 정하느냐에 따라 모수공간에서 얼마나 공격적으로 탐색을 할지가 결정된다. 분산이 너무 크면 높이가 높은 지점을 제대로 탐색하지 못하며, 너무 작으면 한 곳에 불필요하게 오래 머물기 때문에, 모수 공간과 시뮬레이션 결과를 고려하여 적당하게 정하는 것이 중요하다. (finite state space를 가정했는데 proposal이 연속형 정규분포인게 이상하게 다가올 수도 있다. 그러나 컴퓨터에서는 정규분포도 이산형으로 근사한 분포라는 점을 생각하면 큰 무리는 아닌 듯 하다.)

이렇게 사후분포의 샘플을 생성한 결과는 다음과 같다.

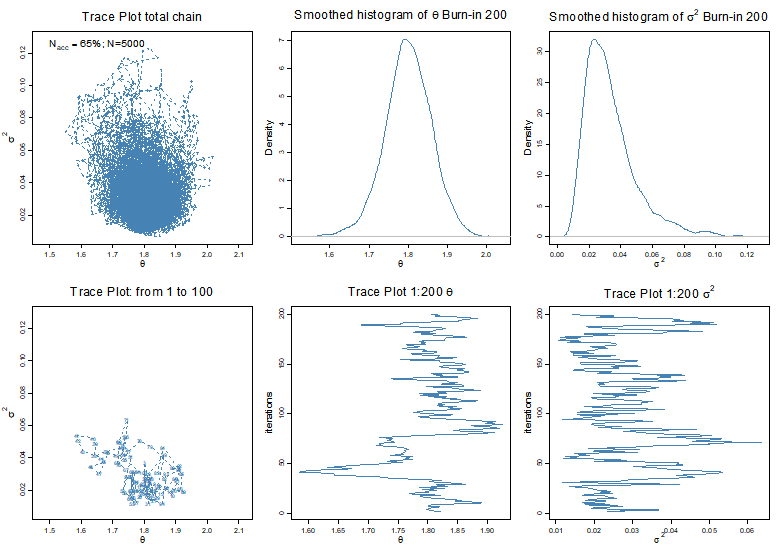
(2,1) 그래프는 모수공간에서 처음 몇번 탐색이 진행되는 경과를 보여준다. 처음에 초기점 주위에서 놀다가 점차 다른 구역으로 뻗어나가는 모습을 볼 수 있다. 이를 각각의 모수에 대해 경과를 보면 (2,2), (2,3) 그래프와 같다. 다만 처음에 생성된 샘플들은 임의로 주어진 초기치의 영향을 많이 받는다. 마코브체인의 극한분포가 실제 분포에 수렴하기 위해서는 충분히 많은 “Burn-in” 기간이 필요하며, 때문에 처음 200개의 샘플들은 최종 결과에서 제외한다. 그렇게 해서 총 5,000개의 샘플로 근사된 사후분포는 (1,1)과 같으며, 이를 각각의 모수에 대해 보면 (1,2)와 (1,3)과 같다. 적분으로는 구할 수 없었던 분포가 비로소 눈에 보이는 것이다.

MH의 신기한 활용: 암호 해독하기!

공부하다보니 MH 알고리즘이 암호해독에 쓰인 경우도 있어 신나서 헐레벌떡 달려가서 보았다. 아래 링크에서 자세히 읽을 수 있다. (그림도 여기서 가져옴)

• https://cims.nyu.edu/~holmes/teaching/asa19/handout_Lecture3_2019.pdf
• https://math.uchicago.edu/~shmuel/Network-course-readings/MCMCRev.pdf

요컨대 말하자면 MH 알고리즘은 crpytography에서의 최적화 문제에서 사용이 가능하다는 것. 여기서는 간략하게 소개하겠다. 다음의 그림과 같은 암호문을 해독해야 한다고 해보자.

암호에 쓰인 문자의 집합을 $S={걁, 굵, 뛠,…}$이라고 하고, 우리가 알아보는 알파벳의 집합을 $A={a,b,c,…}$이라고 하면, 암호를 해독하는 “cipher"라는 것은 다음의 함수를 의미한다.

$$ \phi : S \to A $$

암호분자의 개수와 알파벳의 개수가 같다면, (대문자도 무시하면) 이 함수 $\phi$는 총 $26!$ 가지가 가능하다. 어마무시하게 큰 숫자다. 어떻게 $\phi$를 찾아야 할까? 한 가지 방법은 바로 암호문이 주어졌을 때, 영어 알파벳의 상대빈도를 추정하여 만든 Likelihood를 바탕으로 $\phi$의 분포를 추정하는 것이다.

저 이상한 암호를 쓴 사람이 적어도 영어를 쓴다고 하자. 그렇다면 일반적인 영어 문서에서 자주 등장하는 알파벳들의 빈도와, 저 암호문에서 자주 등장하는 암호문자들의 빈도는 비슷할 것이다. 예컨대 아무 영어 소설책이나 가져와서 노가다로 분석해 모든 알파벳의 상대빈도를 알아내서, 알파벳들의 likelihood 함수를 다음과 같이 만들 수 있다. (여기서 $f$는 각 암호에 대응하는 알파벳이 해독된 암호문에서 등장한 횟수 (혹은 상대빈도) 이다.)

$$ L(x_1, x_2, …, x_n| \phi)=\prod_{i=1}^n f(\phi(x_i)) $$

그럼 여기서 어떤 임의의 $\phi$를 집어 넣었을 때 그 $\phi$의 likelihood를 계산할 수 있으며, 베이즈 정리를 이용하면 $\phi$의 분포 $\pi(\phi)$를 알 수 있다.

$$ \pi(\phi) = \dfrac{L(\phi)}{\sum_{\phi}L(\phi)} $$

이 확률이 높다는 것은 그만큼 암호문자와 알파벳의 상대빈도가 비슷하다는 것이며, 이는 즉 어떤 암호 문자를 어떤 알파벳으로 변환시켰을 때 그 결과를 제법 읽을 수 있다는 것이다. 문제는 이 함수 $\pi(\phi)$를 계산하려면 분모를 알아야 하는데 그러면 계산이 무지막지하다는 것이다. 즉 어떤 분포의 상수배까지만 알고 있는 상황이며, 때문에 MH를 이용해 샘플링을 하여 $\pi(\phi)$를 근사하는 것이다.

여기까지만 보면 “뭔데 ㅆ덕아"라는 말이 절로 나온다. 찬찬히 이해해보자. 알파벳이 $a, b, c$만 있다고 치자. 예컨대 $a$가 100번, $b$가 50번, $c$가 10번 쓰였다고 하자. 그렇다면 이 문서에서 알파벳들이 각각 $i, j, k$번 등장할 확률은 모수가 $\theta_a=\dfrac{10}{16}, \theta_b=\dfrac{5}{16}, \theta_c=\dfrac{1}{16}$인 멀티노미알 분포를 따를 것이고, Likelihood를 다음과 같이 쓸 수 있다. (물론 문서 쪼가리 하나만 보고 전체 영어 문서 중에서 $a, b, c$의 상대빈도의 모수가 $\theta_a=\dfrac{10}{16}, \theta_b=\dfrac{5}{16}, \theta_c=\dfrac{1}{16}$라고 단정할 수는 없지만, 암호 하나 해독하자고 책 1,000권을 읽을 수는 없으니 적당한 책 하나 골라서 그냥 저렇게 추정치를 모수로 때려 넣는거다. )

$$ L(i, j, k|\theta_a=\dfrac{10}{16}, \theta_b=\dfrac{5}{16}, \theta_c=\dfrac{1}{16})= (\dfrac{10}{16})^i (\dfrac{5}{16})^j (\dfrac{1}{16})^k $$

자 이제 어떤 암호해독법칙 ($cipher$) $\phi_1$이 있어서 암호 ${★, ■, ▼}$를 $\phi_1(★)=a, \phi_1(■)=b, \phi_1(▼)=c$로 해독했다고 하자. 그랬더니 암호문($encrpyted ;code$)에 $a$가 10번, $b$가 7번, $c$가 6번 나왔다고 해보자. 그렇다면 $\phi_1$의 Likelihood는 다음과 같이 쓸 수 있겠다.

$$ L(encrypted;code|cipher=\phi_1) = (\dfrac{10}{16})^{10} (\dfrac{5}{16})^7 (\dfrac{1}{16})^6 $$

암호문을 보기 전 cipher의 분포를 uniform하게 주고 (편의상 모두 1), 암호문을 바탕으로 각각의 $\phi$에 대해 위의 식처럼 likelihood를 계산하면, (24)처럼 cipher의 posterior분포를 구할 수 있다. 이때 이 분포를 직접 구하기에는 분모의 상수를 계산하는게 너무 힘드니, MH를 이용해 posterior 분포를 근사하는 것이다. (실제로는 이렇게 한 알파벳의 빈도만 가지고는 해독이 엉망진창이어서, 두 알파벳의 쌍, 예컨대 $(a,b)$, $(b,a)$, $(a,c), …$모든 가능한 쌍의 빈도를 계산해 likelihood를 세웠다고 한다.)

그렇게 하면 위의 마코브 체인이 진행됨에 따라 $\phi$의 샘플이 나올 것이고(위 그림은 셰익스피어의 햄릿 구절을 임의로 암호화하여 해독한 결과), 위의 그림처럼 그에 따라 암호도 다르게 해독될 것이다. 이 샘플들은 $\pi(\phi)$ 분포가 몰려있는 부분 중점으로 많이 나올 것이다. 이 부분에서 가장 Likelihood가 높은 $\phi$를 찾는 것이다. 즉 MCMC를 사용해여 암호의 Likelihood $L(code|\phi)$를 최적화한 것. 그렇게 해서 최종 해석된 암호는 다음과 같다고 한다. 치사하게 영어와 스페인어 등등을 섞어 썼는데도 용케 잘 맞췄다!

2-3. Gibbs Sampler Algorithms

앞서 살펴본 Metropolis-Hastings 알고리즘은 한 지점에서 다른 지점으로 이동을 할 때 임의로 정규분포로 정한 proposial 분포를 사용하였다. 하지만 만일 모수공간을 탐색할 때, 어느 한 모수를 제외한 다른 모든 모수들이 주어졌을 때 그 모수의 확률을 알고 있다면, 즉 모든 모수에 대하여 “full conditional distribution"을 알고 있다면, 굳이 이렇게 임의로 proposal 분포를 사용할 필요 없이 바로 그 조건부분포를 사용할 수 있다. 이렇게 할 경우, MH 알고리즘에서처럼 굳이 accept-reject를 결정할 필요 없이 조건부분포로 생성된 샘플을 바로 마코브 체인의 샘플로 받아들일 수 있는데, 이를 수식으로 보이면 다음과 같다.

full conditional distribution을 알고 있다는 것은 다음을 의미한다.

$$ \begin{align} \text{Random vector}&\quad \mathbf{X} = [X_1, X_2, …, X_N]'\\\
\text{Full conditional distribution}&\quad p(X_i=x|X_j=x_j, ;^\forall j \neq i) \end{align} $$

현재 있는 지점이 $X = [X_1, X_2, …, X_N]$이라고 할때, 이 N개의 좌표 중에서 임의로 ($1/N$의 확률로) $X_i$ 상태를 선택하고, 위에서 주어진 full conditional distribution에 따라 새로운 $X_i^{new}$를 생성한다. 그렇게하여 생성된 $Y= [X_1, X_2, …, X_i^{new}, …,X_N]$를 새로운 지점으로 바로 받아들이는 것이다. 이러한 방식으로 결정된, $X$에서 $Y$로 넘어가는 proposal probability $q_{i,j}$는 다음과 같다.

$$ \begin{align} \text{Proposal Probability}\quad &q_{\mathbf{X},\mathbf{Y}} = \dfrac{1}{N} p(X_i=x|X_j=x_j, ;^\forall j \neq i) = \dfrac{1}{N}\dfrac{p(\mathbf{Y})}{p(X_j=x_j, ;^\forall j\neq i)}\\\
& q_{\mathbf{Y},\mathbf{X}} = \dfrac{1}{N} p(X_i=x|X_j=x_j, ;^\forall j \neq i) = \dfrac{1}{N}\dfrac{p(\mathbf{X})}{p(X_j=x_j, ;^\forall j\neq i)} \end{align} $$

이제 이렇게 정의된 proposal probability를 $\alpha_{X, Y}$의 결정식 (15)에 대입하면 다음과 같이 1이 됨을 알 수 있다.

$$ \alpha_{{\mathbf{X},\mathbf{Y}}} = \min(\dfrac{p(\mathbf{Y}) q_{\mathbf{Y},\mathbf{X}}}{p(\mathbf{X})q_{\mathbf{X},\mathbf{Y}}},1) = \min(\dfrac{p(\mathbf{Y}) p(\mathbf{X})}{p(\mathbf{X})p(\mathbf{Y})},1) =1 $$

때문에 proposal probability를 full conditional distribution으로 정하면, 그 조건부 분포에 따라 생성된 새로운 지점은 언제나 채택되는 것이다!

앞서 등장한 예시를 들어 Gibbs Sampler를 설명해보자.

$$ \begin{align} \text{Likelihood}&\quad D \sim N(\theta, \tilde\sigma^2)\\\
\text{Prior}&\quad \tilde\sigma^2 \sim \Gamma(\nu_0/2, \nu_0\sigma_0^2/2)\\\
&\quad \theta \sim N(\mu_0, \tau_0^2)\\\
\text{Posterior} &\quad p(\theta_i, \tilde\sigma_j^2|D) \propto p(\theta_i, \tilde\sigma_j^2)\times p(D|\theta_i, \tilde\sigma_j^2)\\\
&= dnorm(\theta_i, \mu_0, \tau_0^2)\times dgamma(\tilde\sigma^2_j, \nu_0/2, \nu_0\sigma_0^2/2)\times \prod_{k=1}^N dnorm(x_k, \theta_i, \tilde\sigma^2_j) \end{align} $$

정규분포 에시를 보면, 임의로 평균과 precision의 초기 시작점이 주어져있을 때, 먼저 1) precision이 고정된 상태에서 데이터와 precision이 주어졌을 때의 평균의 분포에 따라 새로운 평균을 추출하고, 2) 그 후 평균이 고정된 상타에서 데이터와 평균이 주어졌을 때의 precision의 분포에 따라 새로운 precision을 추출하는 방식을 계속 반복하는 것이다. (원래는 매번 1/2의 확률에 따라 평균과 precision 중 하나를 택해야 하나, 점근적으로 모든 모수가 뽑힐 확률이 동등하기만 하면 되므로, 편의상 순차대로 뽑는 알고리즘을 써도 무방하다.)

Gibbs Sampler의 코드는 Metropolis Hastings보다 더 간단하다. Proposal 분포를 정하고, 매번 높이를 비교하여 기각하거나 채택하는 과정이 없기 때문이다. 먼저 MH와 같이 데이터와 사전분포를 특정하고, 순차대로 full conditional posterior 분포에 따라 샘플을 생성한다. 이렇게 해서 생성된 결과는 다음과 같다.

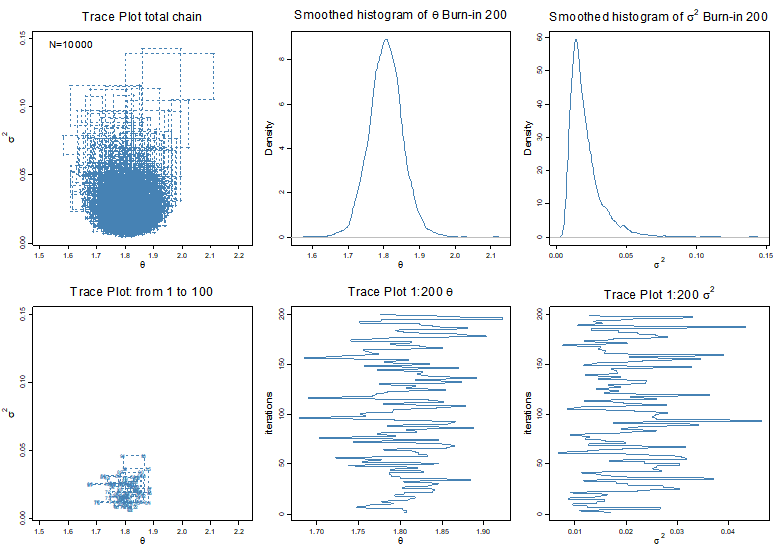
대략적인 근사결과는 Metropolis-Hastings와 같다. 큰 차이점이라고 한다면 매번 샘플이 생성되는 경로가 직각, 즉 axis-aligned 되어있다는 것이다. 이는 proposal 분포가 full condtional distribution이기에, 다른 모든 모수가 고정된 상태에서 하나의 모수에 대해서만 샘플링을 하기 때문에 당연한 결과이다.

2-4. Hamiltonian Monte Carlo

우리가 직접 쓰게될 Stan 프로그램은 샘플링을 할 떄 HMC를 사용하기 때문에, 이게 뭔지 간략하게만 알아보겠다. Gelman의 BDA에 12.4과 Kruschke의 DBDA의 14장을 주로 참고하였다.

HMC가 등장한 이유는 MH가 느리기 때문이다. 왜 느릴까? 기억해보면 MH에서는 일단 한 지점에서 다른 지점으로 점프 (propose)할 때, 우리가 측정하고자 하는 산의 해발고도 $p(\theta|D)$에 상관없이 그냥 노말로 아무때나 간다. 그러니 산에 좀 올라가고 싶으면 땅의 경사를 봐서 높은 곳으로 올라가면 좋은데, 그냥 중심이 현재 지점이 노말분포에 따라 이동하니까 높은 곳을 올라갈 확률이나 낮은 곳으로 내려갈 확률이나 똑같은 것이다. 그래서 빨리빨리 산을 오르지 못한다. HMC는 여기서 porposal을 할 때 산의 경사를 고려해, 더 높은 곳으로 잘 올라가게끔 만든 알고리즘이다.

먼저 MH 알고리즘을 다시 써보자. 시뮬레이션이 이뤄지는 모수 공간에서, 현재 지점을 중심으로 다음 지점으로 이동하는 벡터를 $\phi$라고 하자. 앞서 봤듯이 $\phi$는 노말 분포를 따른다. 그렇게 현재 위치에서 다음 위치로 이동하면, 우리의 관심사 $\theta$는 앞서 설명한 acceptance probability에 따라 업데이트 되거나 기각된다. 따지고 보면 MH는 사실 두 변수 $(\phi, \theta)$가 같이 업데이트 되는 거다.

$$ \begin{align} \text{Proposal:}&\quad \phi \sim MVN(0, M) \quad \text{($M$ diagonal)}\\\
\text{Paremeter:}& \quad \theta \sim p(\theta|D), \quad \text{accepted with }\alpha_{i,j} =\min(\dfrac{p(\theta_j)p(D|\theta_j)}{p(\theta_i)p(D|\theta_i)},1) \end{align} $$

이를 알고리즘 단계로 나타내면, 아무 시작점 $\theta_t$에서

Metropolis-Hastings Algorithm

1. Generate $\phi \sim MVN(0, M)$
2. Let $\theta^* \leftarrow \theta+\phi$
3. Accept $\theta_{t+1}\leftarrow \theta^*$ with probability $\min(\dfrac{p(\theta^*)p(D|\theta^*)}{p(\theta_t)p(D|\theta_t)},1)$

HM이 느린 이유는 2단계 때문이고, 때문에 HMC가 손을 본 부분이 바로 2이다.

쉽게 말하면 HMC는

1. posterior에 음수 로그를 취해 뒤집어서 골짜기를 만들고,
2. 처음 시작점에서 아무 방향으로나 공을 툭 건드려서
3. 일정 시간이 지나고 도착한 지점을 평가하는 것.

자세히 써보면, 똑같이 아무 시작점 $\theta_t$에서

Hamiltonian Monte Carlo Algorithm

1. Generate $\phi_t \sim MVN(0, M)$ HMC에서 $\phi$는 방향과 속도의 의미를 동시에 가진다. 모멘텀 벡터라고도 부른다. 맨 처음 시작점에서 아무 방향으로나 톡 건드리는데, 톡 건드리는 방향과 건드리는 세기가 바로 여기서 결정된다.

2. Leapfrog steps: 깔짝이 Let $\phi \leftarrow \phi_t, \theta \leftarrow \theta_t$

   leapfrog가 뭔가 해서 찾아봤는데 이거다. 한번에 확 멀리 뛰지 않고 저렇게 한 놈씩 제껴가면서 깔짝깔짝 넘어가는 건데, HMC에서 방향을 찾는 방법과 비슷하다. 나는 그냥 깔짝이라고 하겠다. HM에서는 한번 $\phi$가 뽑히면 그냥 뽑힌 그대로 머얼찍이 한번 뛰어가고 마는데, HMC에서는 매번 기울기를 보면서 깔짝 깔짝 뛰어가는 것.

   

   1. At $\theta$, calculate $\nabla -\log p(\theta|D)$ (unnormalized) posterior는 몰라도 그 상수배인 prior x likelihood는 아니까 그냥 상수배 무시하고 그라디언트를 구한다. 모수 공간에서 높아지는 방향으로는 그라디언트가 양수일 것이고, 낮아지는 방향으로는 음수가 될 것이다. 음수 로그니까 우리는 낮아지는 방향으로 가고 싶을 거다.
   2. Make a half step: $\phi \leftarrow \phi-\dfrac{1}{2}\epsilon\nabla \log p(\theta|D) $ 그라디언트에 따라서 모멘텀 벡터를 $\frac{1}{2} \epsilon$만큼 수정한다. 낮은 쪽으로 가는게 목적이니, 기울기가 양수이면 (즉 가는 방향이 오르막길이면) 반대 방향으로 가고, 기울기가 음수이면 (가는 방향이 내리막길이면) 그대로($-\times -=+$) 가면 된다. 그렇게 되면 원래 모멘텀 벡터는 원래 방향 $\phi$에서, 좀 더 로그 음수 posterior가 낮은 쪽으로 방향을 틀어 $(\nabla \log p(\theta|D))$, $\frac{1}{2} \epsilon$만큼 더 갈 것이다.
   3. Move with momentum: $\theta \leftarrow \theta - \epsilon M^{-1} \phi$ 2에서 기울기에 따라 수정된 $\phi$에 따라 $\theta$를 이동한다. 이렇게 이동한 이유는, 새로 이동한 지점에서 다시 기울기를 계산해 또 낮은 방향으로 방향을 틀기 위함이다. $M^{-1}$은 그냥 대각행렬이고, 모수 공간의 각 축마다 스케일을 다시 맞춰준다고 생각하면 된다.
   4. Repeat from 1 to 3 for $L$ times to get $\theta^{*}, \phi^{*}$

   왜 이러는 걸까? 사실 HMC가 정말 하고 싶은 것은 음수로그분포(골짜기)를 따라 툭 건들었더니 도로록 내려가는 공을 시뮬레이션 하는거다. 그렇게 해서 공을 적당히 굴리다가 멈추고, 그 멈춘 지점을 새로운 proposal로 받아들이고 싶은 거다. 이렇게 생각하면 음수로그분포 $-\log p(\theta|D)$는 마치 “위치 에너지”, 모멘텀 벡터의 $-\log p(\theta)$는 마치 “운동 에너지"로 볼 수 있다. 그러나 컴퓨터가 이산 공간이니 잠깐 갔다가 다시 방향 틀어서 잠깐 가는 과정을 $L$번 돌려서 최대한 연속적인 움직임을 근사하는 것이다.

3. Accept $\theta_{t+1}\leftarrow \theta^{*}$ with probability $\min(\dfrac{p(\theta^{*})p(D|\theta^{*})p(\phi^{*})}{p(\theta_t)p(D|\theta_t)p(\phi_t)},1)$

   만일 정말로 연속적으로 움직이는 공을 시뮬레이션 했다면 모든 지점에서 위치에너지와 운동에너지의 합은 일정할테니 새로운 샘플은 항상 받아들여질 것이다. 그러나 이산형이기 때문에 근사 오차가 있다. 만일 매번 깔짝대는 만큼인 $\epsilon$이 작으면 근사 오차가 줄어서 샘플이 잘 받아들여지겠지만, 그만큼 멀리 가기까지 오래 걸려서 $L$이 커야 하고, 때문에 연산을 많이 해야할 것이다. (대개 65% 정도 생각하고 $\epsilon$을 잡는다고 한다.)

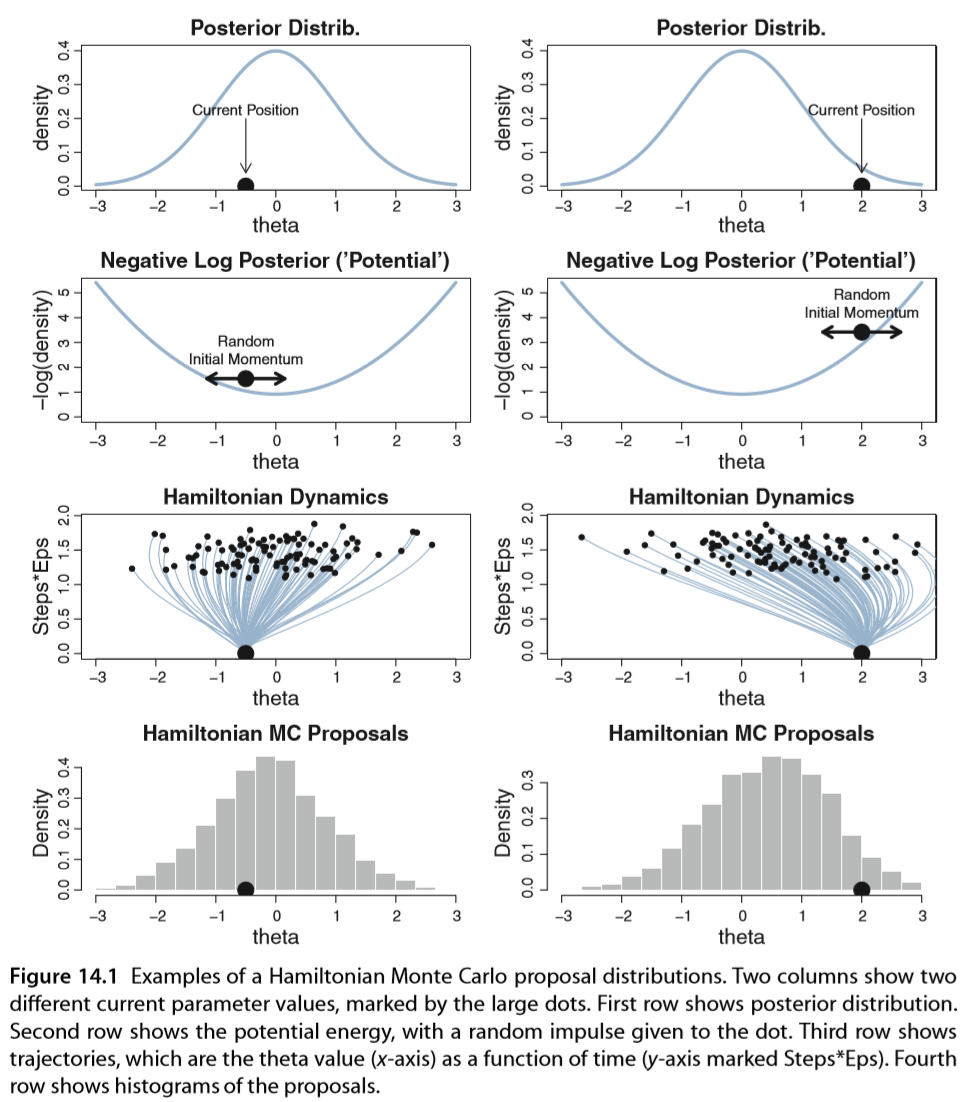
이 과정을 그림으로 나타낸게 아래 그림이다(Kruschke, 2015). 세 번재 줄의 수많은 갈래들 하나하나는 한 번 시행마다 $\phi$가 수정되면서 $\theta$가 수정되는 궤적을 나타낸다. 그 갈래들의 종착역을 히스토그램으로 나타낸게 맨 마지막 줄이다. 보면 분포의 중심이 posterior가 높은 곳을 향해 치우친 것을 볼 수 있다. 그래서 MH에 비해 수렴 속도가 빠른 것이다.

(출처: Doing Bayesian Data Analysis, Kruschke)

HMC에서 내가 조정할 파라미터는 크게 1) 프로포절 분포의 공분산 $M$, 2) 얼마나 오래 공을 굴릴 것인지 $L, \epsilon$인데, 이걸 잘못 설정하면 다음과 같은 참사가 발생한다. 왼쪽 그림을 공을 너무 오래 굴린 경우고, 오른쪽 그림은 공을 처음에 너무 약하게 건들거나 너무 세게 친 경우이다.

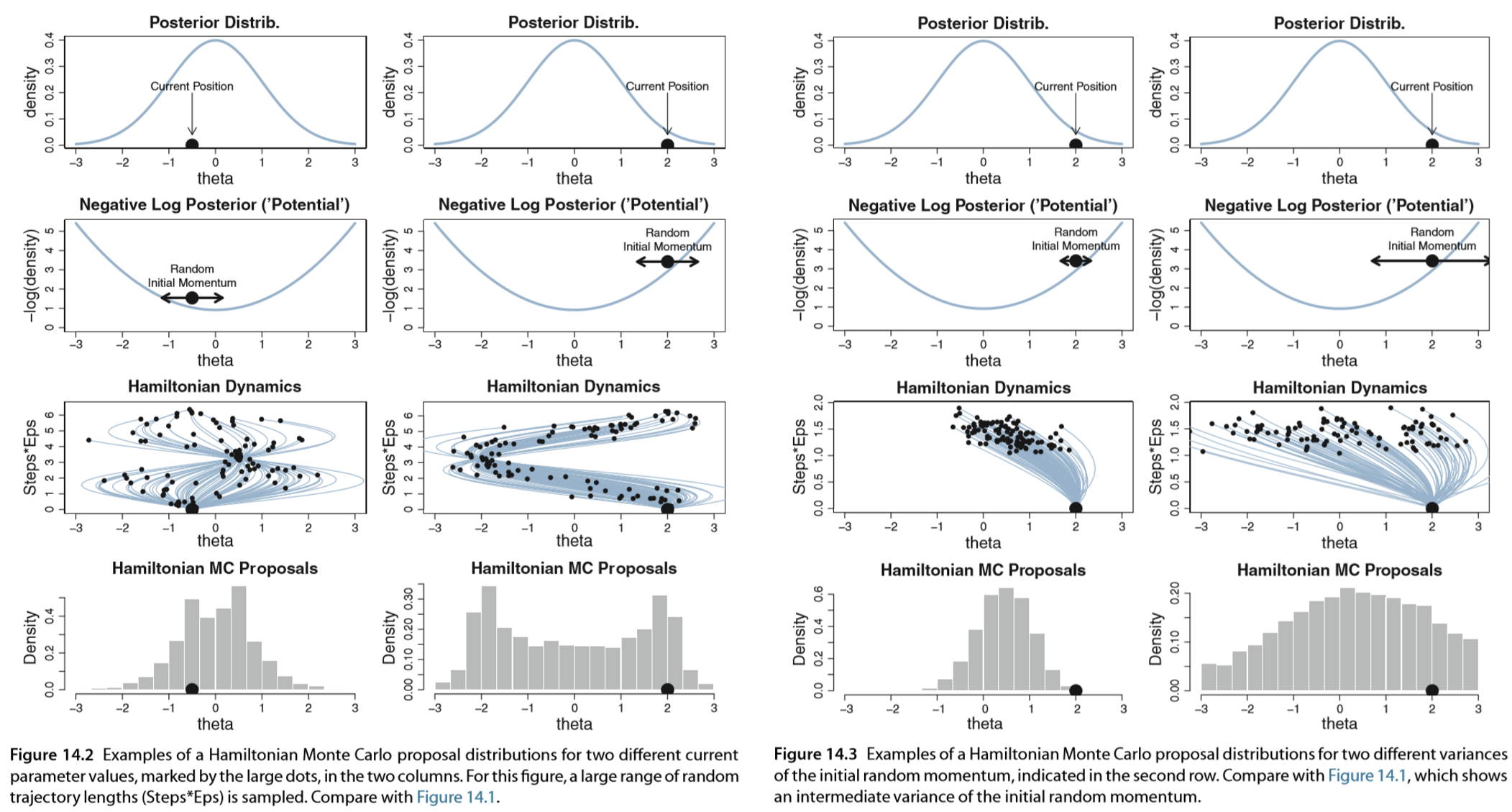
(출처: Doing Bayesian Data Analysis, Kruschke)

HMC를 R에서 실제로 생 코드로 돌려볼 수 있다. 코드는 다음의 링크를 참조: https://jonnylaw.rocks/blog/hamiltonian_monte_carlo_in_r/

3. MCMC diagnostics

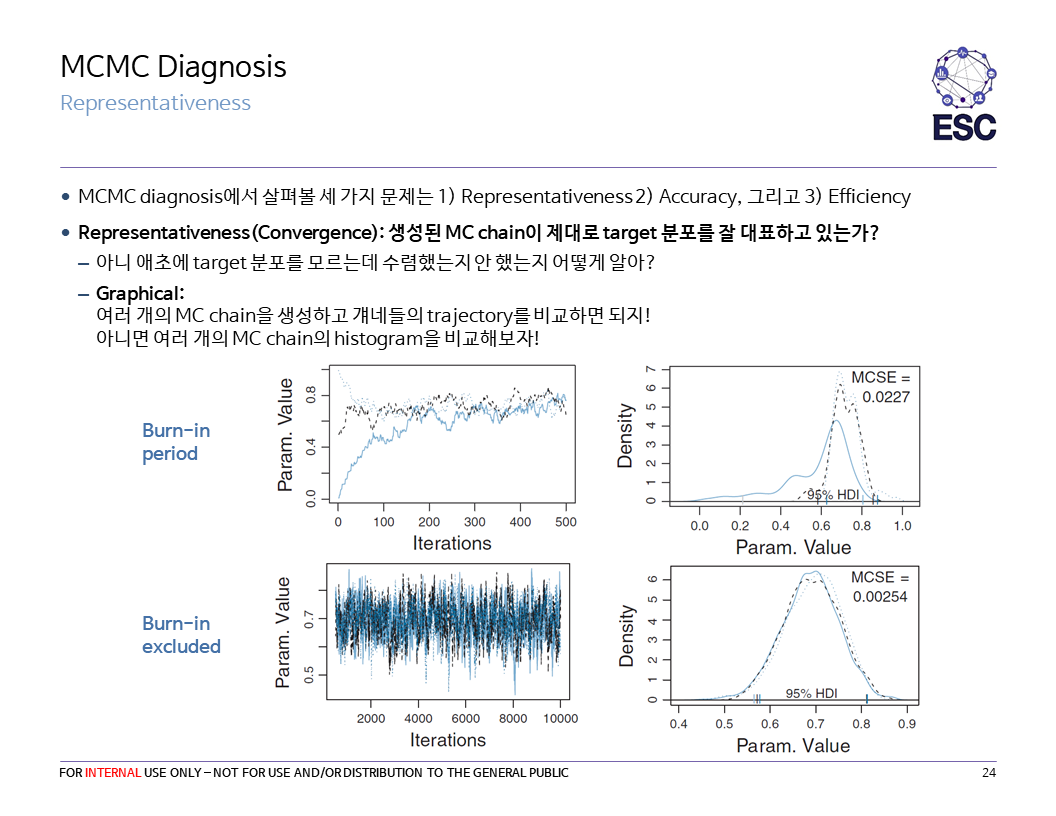
MCMC의 단점은 크게 1) 생성된 샘플들 간에 상관관계가 높으며, 2) 당최 언제 수렴하는지 알 수가 없다는 것이다. 마코브 체인의 극한 분포 정리가 말해주는 것은 그냥 transiton probability만 제대로 설정했다면, 한없이 무한정으로 돌리다보면 각 상태 (모수)의 출현빈도(경험분포)가 극한분포인 사후분포로 수렴한다는 것이다. 그러나 수렴하기까지 얼마나 많이 돌려야하는지 ($n$), 또 한 체인 말고 여러 체인을 돌리면 얼마나 돌려야 하는지($m$)에 대해서는 정말 아무도 모른다. 우리가 할 수 있는 것은 각각의 체인마다 각각의 모수에 대해 trace plot을 그려서 눈으로 확인해보고, 수렴이 적당히 되었는지 체인에서 어떤 통계량을 계산해보고 가늠하는 것 뿐이다. 그렇게 해서 대충 수렴한 것 같으면 $n, m$이 뭐이 어드레 간에 그냥 신경을 끄고 결과를 받아들이는 것 (“Sometimes you don’t care”).

(출처: http://www.robots.ox.ac.uk/~fwood/teaching/C19_hilary_2015_2016/mcmc.pdf)

(하나의 긴 체인을 돌려도 수렴을 잘 못하는 것 같으면 대신 출발 지점을 여러 개로 해서 여러 체인을 돌려 그 체인들을 합쳐야 한다는 의견이 있다. 하지만 이 의견을 까는 사람도 있는데, “하나의 긴 체인에서 답이 안 나오면 여러 개의 짧은 체인을 돌리는 것도 부질없다"라고 한다. http://users.stat.umn.edu/~geyer/mcmc/one.html)

그래서 지금부터는 MCMC 결과의 진단법에 대해 간단히 알아보겠다. 자료는 19년 2학기 베이즈 세션 때 본인이 만든 슬라이드를 그대로 사용한다.

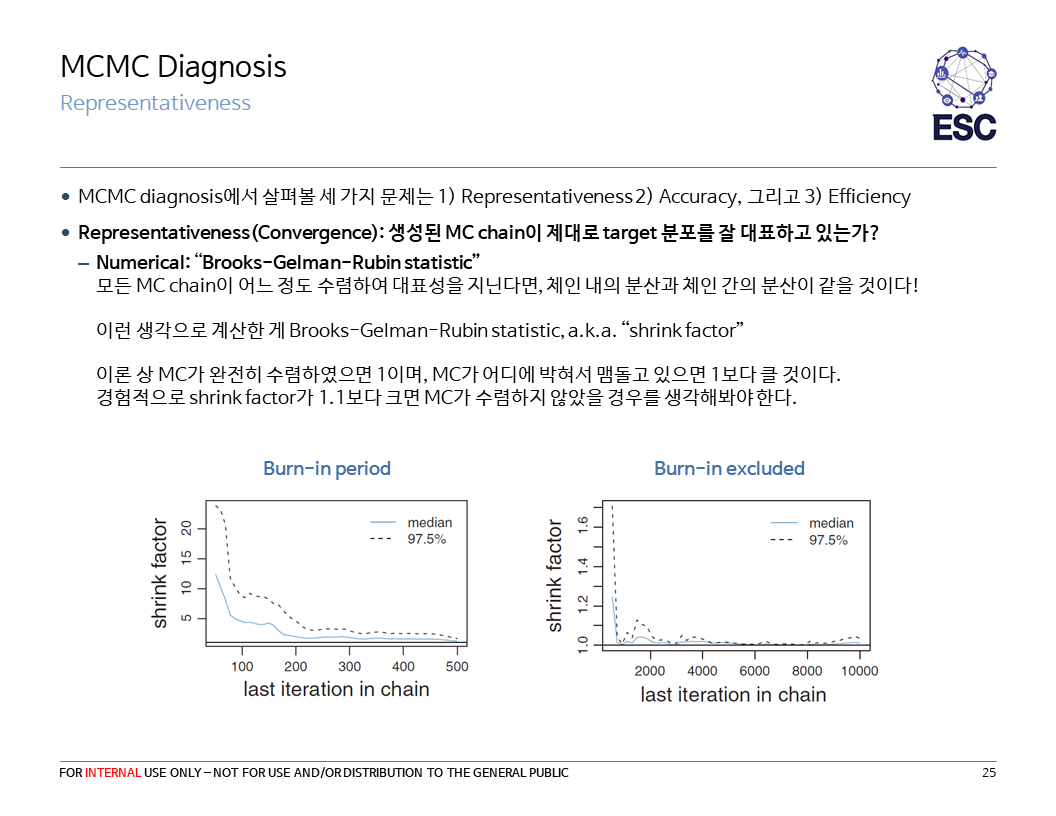
Brooks-Gelman-Rubin statistic에 대해 부연설명을 하겠다.

• $m$개의 크기 n인 체인 내에서 각각 체인 내 분산을 $s^2_j=\dfrac{1}{n-1}\sum_{i=1}^n (\theta_{ij}-\bar{\theta}_j)^2$로 계산하여, $W=\dfrac{1}{m}\sum_{j=1}^m s^2_j$로 모든 체인에 걸쳐 평균을 내리면, $W$는 “체인 내 분산"을 나타내는 통계량이 된다.

• 각 체인 마다의 평균 $\bar{\theta}_j$ 을 또 m개에 걸쳐 평균을 내 $\bar{\theta}$를 계산하자.

  그러고 $B=\dfrac{n}{m-1} \sum_{j=1}^m(\bar{\theta}_j-\bar{\theta})^2$을 계산하면 이건 “체인 간 분산"을 나타내는 통계량이다.

• 이제 $\hat{V(\bar{\theta})} = (1-1/n)W + B/n$으로 정의하자.

  • $E[W]=E[B]= E[s_j^2]=\sigma^2$이므로 $E[\hat{V(\theta)}] = (1-1/n)\sigma^2 + \sigma^2/n = \sigma^2$가 될 것이다. 즉 $\hat{V(\bar{\theta})}$은 unbiased estimator이다.
  • 그러나 실제로는 각 체인마다 시작점이 다 다르니 (overdispension) $B$가 크고, $n$이 커지면서 점점 줄어들 것이다.
  • 때문에 $\sqrt{\hat{V(\bar{\theta})}/W}$은 처음에는 1보다 크다가, 수렴이 잘 되었으면 1으로 위에서 수렴한다. 이걸 BGR statistics라고 한다. (BGR stat이 1에 가까워지는 시점을 기준으로 Burn-in을 판단하기도 한다.)

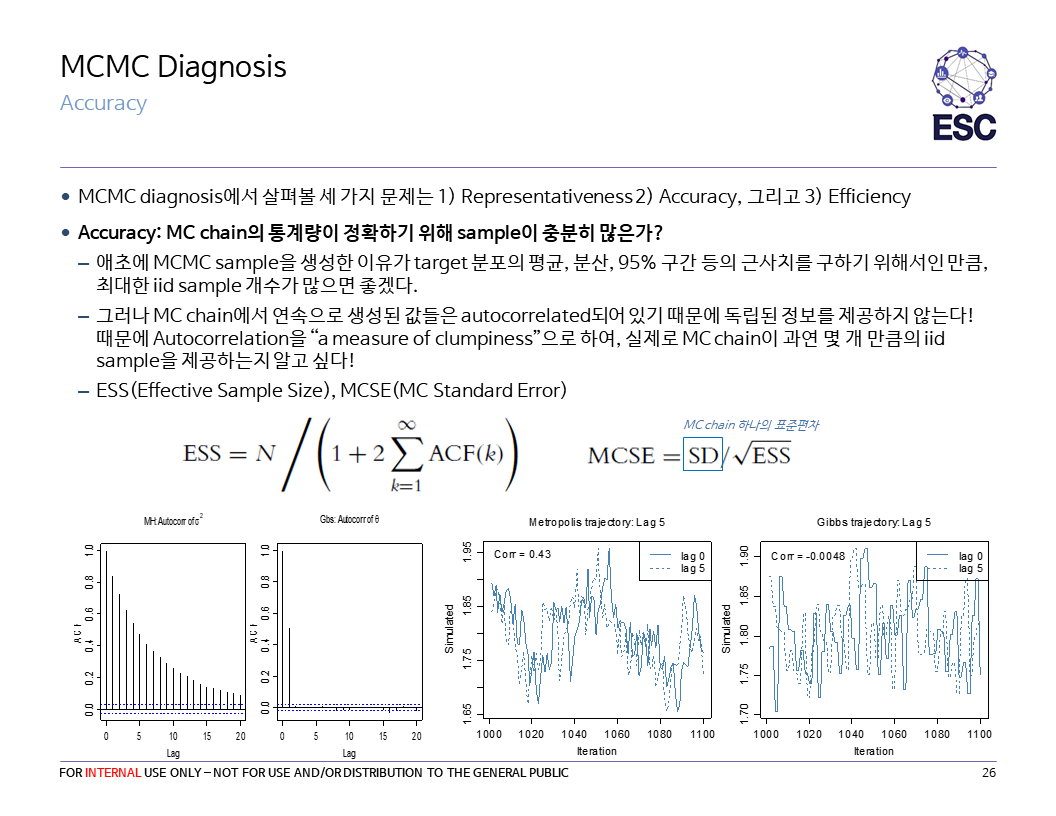
ESS에 대해서 부연 설명을 하자면 $ESS = \dfrac{N}{\sum_{-\infty}^{\infty} \rho_t}=\dfrac{N}{1+2\sum_{t=1}^{\infty} \rho_t}$이며, 만일 모든 $t>1$에 대해 $\rho_t=1$이면 $ESS=1$, $\rho_t=0$이면 $ESS=N$.

그래서 thinning을 해야함? 딱히… 오히려 estimation의 정확성을 낮춘다고 하네

On thinning of chains in MCMC - Link - 2012 - Methods in Ecology and Evolution - Wiley Online Library

References

1. Hoff, P. D. (2009). A first course in Bayesian statistical methods. New York: Springer.

2. Kruschke, J. K. (2015). Doing Bayesian data analysis: A tutorial with R, JAGS, and Stan. Burlington, MA: Academic Press.

3. Ross, S. M. (2013). Simulation. San Diego: Academic Press.

4. https://cims.nyu.edu/~holmes/teaching/asa19/handout_Lecture3_2019.pdf (암호해독 예시)

5. https://math.uchicago.edu/~shmuel/Network-course-readings/MCMCRev.pdf (암호해독 예시)

6. https://jonnylaw.rocks/blog/hamiltonian_monte_carlo_in_r/ (HMC R로 직접 해보기)

7. http://www.robots.ox.ac.uk/~fwood/teaching/C19_hilary_2015_2016/mcmc.pdf (MCMC 문제점 관련)

8. http://users.stat.umn.edu/~geyer/mcmc/one.html (MCMC 진단 관련)

9. http://patricklam.org/teaching/convergence_print.pdf (MCMC 진단 관련)