Bayesian Hierarchical Modeling and its Applications
여러 모수를 한 묶음으로 묶어주는 Hyperparameter

Review: Full conditional posterior for normal likelihood
일단 정규분포의 semi-conjugate prior에 대한 내용을 다시 정리해보자.
- $p(\theta\mid\sigma^2, \mathbf{D}) = dnorm(\theta, \mu_n, \tau_n^2)$
- $\mu_n= \dfrac{1/\tau_0^2}{\frac{1}{\tau_0^2} + \frac{n}{\sigma^2}}\mu_0 + \dfrac{\frac{n}{\sigma^2}}{\frac{1}{\tau_0^2} + \frac{n}{\sigma^2}}\bar{x}$
- $\tau_n^2 = \dfrac{1}{\frac{1}{\tau_0^2} + \frac{n}{\sigma^2}}$
- $p(\sigma^2\mid\theta, \mathbf{D}) = dinv\Gamma(\sigma^2, v_n, \dfrac{1}{v_n}(v_0\sigma_0^2+\sum (y_i-\theta)^2)$
Two Group Comparison: Math scores
library(ggplot2)
library(cowplot)
school1 = dget('http://www2.stat.duke.edu/~pdh10/FCBS/Inline/y.school1')
school2 = dget('http://www2.stat.duke.edu/~pdh10/FCBS/Inline/y.school2')
df = data.frame(school = c(rep('s1', length(school1)),rep('s2', length(school2))),
score = c(school1, school2)
)
ggplot(df, aes(x=school, y=score))+
geom_boxplot(aes(fill=school))+
ggtitle('Math scores comparison')+
theme_cowplot()
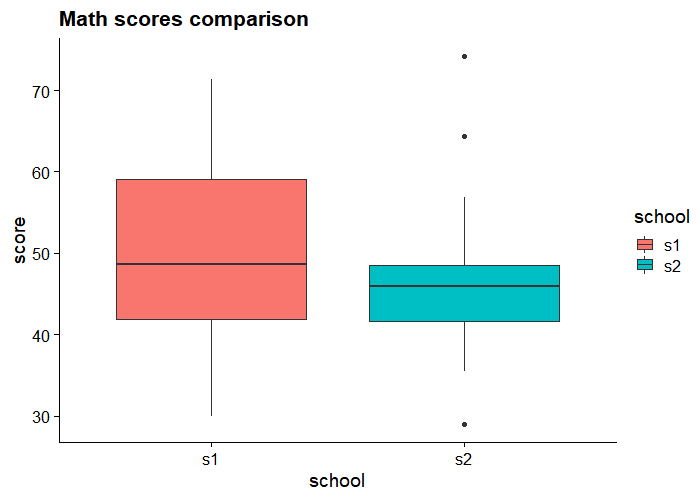
통계학이 필요한 이유는 이런 “애매한” 차이 때문이다. 딱 봐도 눈에 훤히 보이게 다르면 누가 통계학자를 찾겠나.
빈도론자들이 하는 two-sample t-test는 다들 배웠을 것이다. 그런데 어떻게 두 집단의 평균이 완전히 똑같거나 아니면 절대 다르거나 둘 중 하나만 가능하냐, 어색하다, 생각할 수도 있다. 그러니까 수식으로 말하면 빈도론자들의 방법은, 학교1의 모평균을 $\hat{\theta_1} = w \bar{y_1}+(1-w) \bar{y_2}$로 추정하고, $w$는 다음과 같이 정한다는 것이다.
$$
w = \begin{cases}
1 \quad &if \quad p-value<0.05\
\dfrac{n_1}{n_1+n_2} \quad &o.w.
\end{cases}
$$
이렇게 너무 극단적으로 정하기보다, 학교들의 상대적인 표본 수, 학교들 표본의 sampling variability 등 다양한 요소들을 고려해서 $w$가 취할 수 있는 값들의 연속적인 분포를 한번 그려보자는 것이 베이지안 추론의 접근이다.
베이지안 프레임워크에 맞춰서 이 문제를 해석하면 다음과 같다.
Likelihood
$$
\begin{align}
y_{1,i} &\sim N(\mu+\delta, \sigma^2)\\\
y_{2,i} &\sim N(\mu-\delta, \sigma^2)\\\
p(D|\mu,\delta, \sigma^2)&= \prod_{i=1}^{n_1}dnorm(y_{1,i}, \mu+\delta, \sigma^2)
\prod_{j=1}^{n_2}dnorm(y_{2,j}, \mu-\delta, \sigma^2)
\end{align}
$$
Prior
$$
\begin{align}
p(\mu, \delta, \sigma^2) &= p(\mu)p(\delta)p(\sigma^2)\\\
\mu &\sim N(\mu_0, \gamma_0^2)\\\
\delta &\sim N(\delta_0, \tau_0^2)\\\
\sigma^2 &\sim inv\Gamma(\nu_0/2, \nu_0\sigma^2_0/2)
\end{align}
$$
Full conditional posterior
$$
\begin{align}
\mu \mid D, \delta, \sigma^2 &\sim \mathcal{N}(\mu_n, \gamma_n^2)\\\
\mu_n &= \gamma_n^2 \times \left[ \mu_0 / \gamma_0^2 + \sum_{i = 1}^{n_1} (y_{i, 1} - \delta) / \sigma^2 + \sum_{i = 1}^{n_2}(y_{i, 2} + \delta) / \sigma^2 \right]\\\
\gamma_n^2 &= \left[ 1/\gamma_0^2 + (n_1 + n_2) / \sigma^2 \right]^{-1}\\\
\delta \mid D, \mu, \sigma^2 &\sim \mathcal{N}(\delta_n, \tau_n^2)\\\
\delta_n &= \tau_n^2 \times \left[ \delta_0 / \tau_0^2 + \sum_{i = 1}^{n_1} (y_{i, 1} - \mu) / \sigma^2 - \sum_{i = 1}^{n_2} (y_{i, 2} - \mu) / \sigma^2 \right]\\\
\tau_n^2 &= \left[ 1 / \tau_0^2 + (n_1 + n_2) / \sigma^2 \right]^{-1}\\\
\sigma^2 \mid D, \mu, \delta &\sim inv\Gamma(\nu_n / 2, \sigma_n^2 \nu_n / 2)\\\
\nu_n &= \nu_0 + n_1 + n_2\\\
\nu_n \sigma_n^2 &= \nu_0 \sigma_0^2 + \sum_{i = 1}^{n_1} (y_{i, 1} - \left[\mu + \delta \right])^2 + \sum_{i = 1}^{n_2} (y_{i, 2} - \left[ \mu - \delta \right])^2
\end{align}
$$
수식만 보면 기겁을하게 생겼는데 사실 다 노말 분포의 full conditional posterior가 뭔지만 알면 큰 어려움 없이 유도할 수 있다. 이제 이렇게 각 모수에 대한 full conditional posterior를 구했으니 깁스 샘플러를 돌릴 수 있다. 코드는 교재를 참고하자.
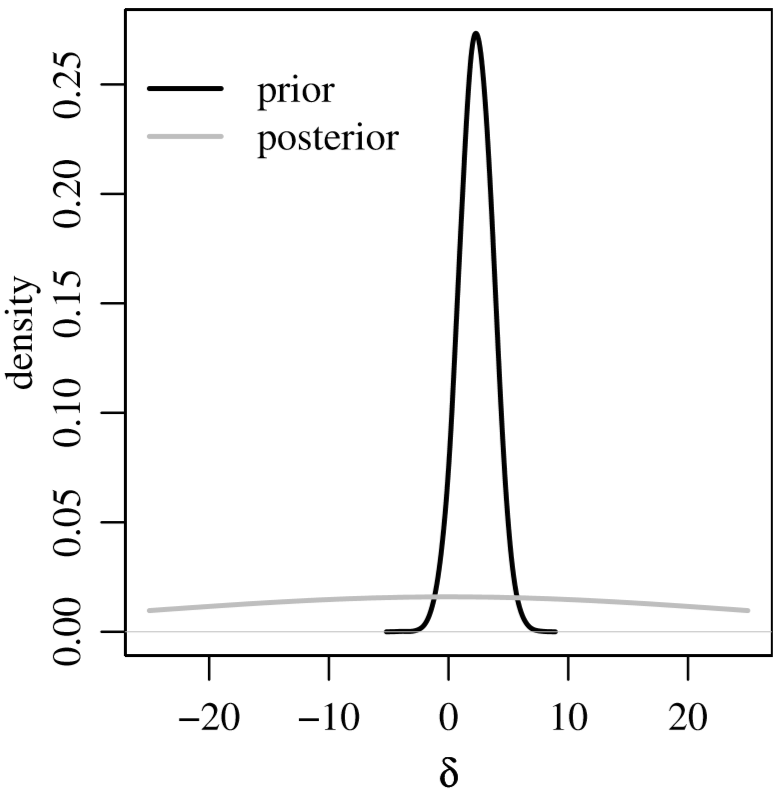
중요한 것은, 베이지안에서 두 그룹의 평균 차이가 유의미한지 보는 것은 결국 $\delta$의 사후분포를 보는 것과 같다는 점이다. 깁스 샘플러의 매번 반복 횟수마다 모수를 생성하고, 그 모수에 대해 샘플을 생성해, 다음과 같은 통계량 $\hat{p}(d>0|D), \hat{p}(Y_1 > Y_2|D)$을 전체 샘플 중에서의 상대빈도로 구할 수 있다.
(Hoff, p.130)
Bayesian Hierarchical Model for Multiple Comparisons
만일 두 개 이상의 여러 집단 ${\mathbf{Y}_1, \mathbf{Y}_2, …, \mathbf{Y}_m}$간의 평균 ${\theta_1, \theta_2, …, \theta_m}$을 비교한다고 해보자. 이때 데이터에 대해 다음과 같은 가정을 세운다고 하자.
$$
\begin{align}
p(y_j\mid \theta_j, \sigma^2) &= dnorm(y, \theta_j, \sigma^2) \quad \text{within group model}\\\
p(\theta_j\mid \mu, \tau^2) &= dnorm(\theta_j, \mu, \tau^2) \quad \text{between group model}
\end{align}
$$
데이터에 대한 이러한 모델은 다음의 가정을 내포하고 있다.
- 한 그룹 내에서 관측치들은 동일한 분포를 따르는 독립인 샘플이다.
- 각 그룹별 평균도 또한 동일한 분포를 따르는 독립인 샘플이다.
이러한 가정이 타당한 이유는 de Finetti’s theorem에서 찾을 수 있다. 어떤 데이터 열의 확률 $p({x_1, x_2, …, x_n})$ 이 그 데이터 열의 순서를 바꿔도, 즉 모든 가능한 permutation에 대해 그 데이터 열의 확률이 변하지 않을 때 이 데이터들이 exchangeable하다고 한다. 드핀티 정리란, 이렇게 exchangeable한 데이터들은 서로 독립이 아닐지라도 어떤 모수가 주어지면 조건부 독립으로 볼 수 있다는 말이다.
de Finetti’s theorem
다음 두 조건은 동치이다.
- ${x_1, x_2, …, x_n}$은 exchangeable하다.
- 어떤 모수 $\boldsymbol{\theta} \sim p(\boldsymbol{\theta})$가 있어 다음이 성립한다; ${x_1, x_2, …, x_n \mid \boldsymbol{\theta} } \sim^{iid} p(\mathbf{x}\mid \boldsymbol{\theta})$
여러 집단의 평균을 비교하는 문제에서도, 한 집단 내에 샘플들은 서로 exchangeable하고, 또 샘플의 모평균끼리도 exchangeable하다. 때문에 (24), (25)와 같은 가정이 충분히 가능한 것이다.
위 가정에서 모수 $\boldsymbol{\theta}$는 $\mu, \tau^2, \sigma^2$이다. 이 모수에 대해 다음의 prior를 줄 수 있다.
$$
\begin{align}
\sigma^2 &\sim inv\Gamma(\nu_0 / 2, \sigma_0^2 \nu_0 / 2) \\\
\tau^2 &\sim inv\Gamma(\eta_0 / 2, \tau_0^2 \eta_0 / 2) \\\
\mu &\sim N(\mu_0, \gamma_0^2)
\end{align}
$$
뭔가 식이 되게 많아져서 복잡해보이는데, 이걸 그림으로 나타내면 다음과 같다.
이렇게 Likelihood와 Prior를 세우고 나면 Posterior는 어떻게 구할 수 있을까? 일단 써보자.
$$
\begin{align}
p(\theta_{j=1}^m, \mu, \tau^2, \sigma^2 \mid \mathbf{D})
&\propto p( \mu, \tau^2, \sigma^2); p(\theta_{j=1}^m\mid \mu, \tau^2, \sigma^2); p(\mathbf{D}\mid\theta_{j=1}^m, \mu, \tau^2, \sigma^2)\\\
&= p(\mu)p(\tau^2)p(\sigma^2);\prod_{j=1}^m p(\theta_j \mid \mu, \tau^2) \prod_{j=1}^m \prod_{i=1}^{n_j} p(y_{j,i}\mid \theta_j, \sigma^2)
\end{align}
$$
(29)에서 (30)으로 넘어가는 과정에서 갸우뚱했을 것이다. 하나씩 살펴보자.
- $p( \mu, \tau^2, \sigma^2) = p(\mu)p(\tau^2)p(\sigma^2)$ 이건 prior를 독립으로 줘서 그렇다. 자명함.
- $p(\theta_{j=1}^m\mid \mu, \tau^2, \sigma^2)=\prod_{j=1}^m p(\theta_j \mid \mu, \tau^2)$ $\theta_j$는 그룹의 평균이다. 그룹의 평균은 우리가 (25)에서 오직 $\mu, \tau^2$에만 의존한다고 했다. 때문에 $\sigma^2$와 독립이므로, 조건 항에서 뺄 수 있는 것이다. 이는 위에 그림을 보면 잘 보인다. 위의 그림에서 화살표로 직접적으로 이어져있지 않는 변수들은 모두 독립이다. 직관적으로 생각해보면, $\mu, \tau^2$의 값을 알면 우리는 $\theta_j$의 분포를 아는 것이니 $\theta_j$에 대해서도 어느정도 알게 된다. 그러나 $\sigma^2$를 안다고 해서 아무것도 변하는 것은 없다.
- $p(\mathbf{D}\mid\theta_{j=1}^m, \mu, \tau^2, \sigma^2) = \prod_{j=1}^m \prod_{i=1}^{n_j} p(y_{j,i}\mid \theta_j, \sigma^2)$ $\mu, \tau^2$는 화살표를 두 번 타고 가면 $Y$에 이어지기 때문에 잘 납득이 안 될 수도 있다. 그러나 $Y_j$에 대하여 $\mu, \tau^2$가 줄 수 있는 정보는 이미 $\theta_j$에 모두 담겨 있다. 때문에 $\theta_j$를 알고 있다면 $\mu, \tau^2$ 따위 알던 모르던 상관이 없는 것이다.
이제 식 (30)을 이용하면 각 모수의 full conditional posterior가 다음에 비례함을 쉽게 알 수 있다. 예컨대 $\mu$의 full conditional posterior이라는 것은 데이터와 다른 모수들이 모두 상수로 주어졌다는 것이다. 때문에 식 (30)에서 $\mu$가 포함되지 않은 식은 모두 상수 취급하여 $\propto$로 없애버릴 수 있는 것이다.
$$
\begin{align}
p(\mu \mid \theta_{j=1}^m, \tau^2, \sigma^2, \mathbf{D})
&\propto p(\mu)\prod_{j=1}^m p(\theta_j \mid \mu, \tau^2)\\\
p(\tau^2 \mid \theta_{j=1}^m, \mu, \sigma^2, \mathbf{D})
&\propto p(\tau^2)\prod_{j=1}^m p(\theta_j \mid \mu, \tau^2)\\\
p(\theta_j \mid \mu, \tau^2, \sigma^2, \mathbf{D})
&\propto p(\theta_j\mid\mu, \tau^2) \prod_{j=1}^m \prod_{i=1}^{n_j} p(y_{j,i}\mid \theta_j, \sigma^2)\\\
p(\sigma^2 \mid \theta_{j=1}^m, \mu, \tau^2, \mathbf{D})
&\propto p(\sigma^2) \prod_{j=1}^m \prod_{i=1}^{n_j} p(y_{j,i}\mid \theta_j, \sigma^2)
\end{align}
$$
이 경우 각 모수들은 어차피 노말 혹은 인버스 감마를 따르기 때문에, 사후분포도 다음과 같이 유도할 수 있다.
$$
\begin{align}
{\mu \mid \theta_{j=1}^m, \tau^2} &\sim N\left(\frac{m\bar{\theta} / \tau^2 + \mu_0 / \gamma_0^2}{m/\tau^2 + 1 / \gamma_0^2}, \left[m / \tau^2 + 1 / \gamma_0^2 \right]^{-1}\right) \\\
{\tau^2 \mid \theta_{j=1}^m, \mu} &\sim inv\Gamma\left(\frac{\eta_0 + m}{2}, \frac{\eta_0\tau_0^2 + \sum_{j = 1}^{m}(\theta_j - \mu)^2}{2} \right) \\\
{\theta_j \mid \mathbf{D}, \sigma^2} &\sim N\left(\frac{n_j\bar{y}_j / \sigma^2 + 1 / \tau^2}{n_j / \sigma^2 + 1 / \tau^2}, \left[ n_j / \sigma^2 + 1 / \tau^2 \right]^{-1} \right) \\\
{\sigma^2 \mid \theta_{j=1}^m, \mathbf{D}} &\sim inv\Gamma\left(\frac{1}{2}\left[ \nu_0 + \sum_{j = 1}^m n_j\right], \frac{1}{2}\left[\nu_0\sigma_0^2 + \sum_{j = 1}^{m} \left( \sum_{i = 1}^{n_j} (y_{i, j} - \theta)^2 \right) \right] \right)
\end{align}
$$
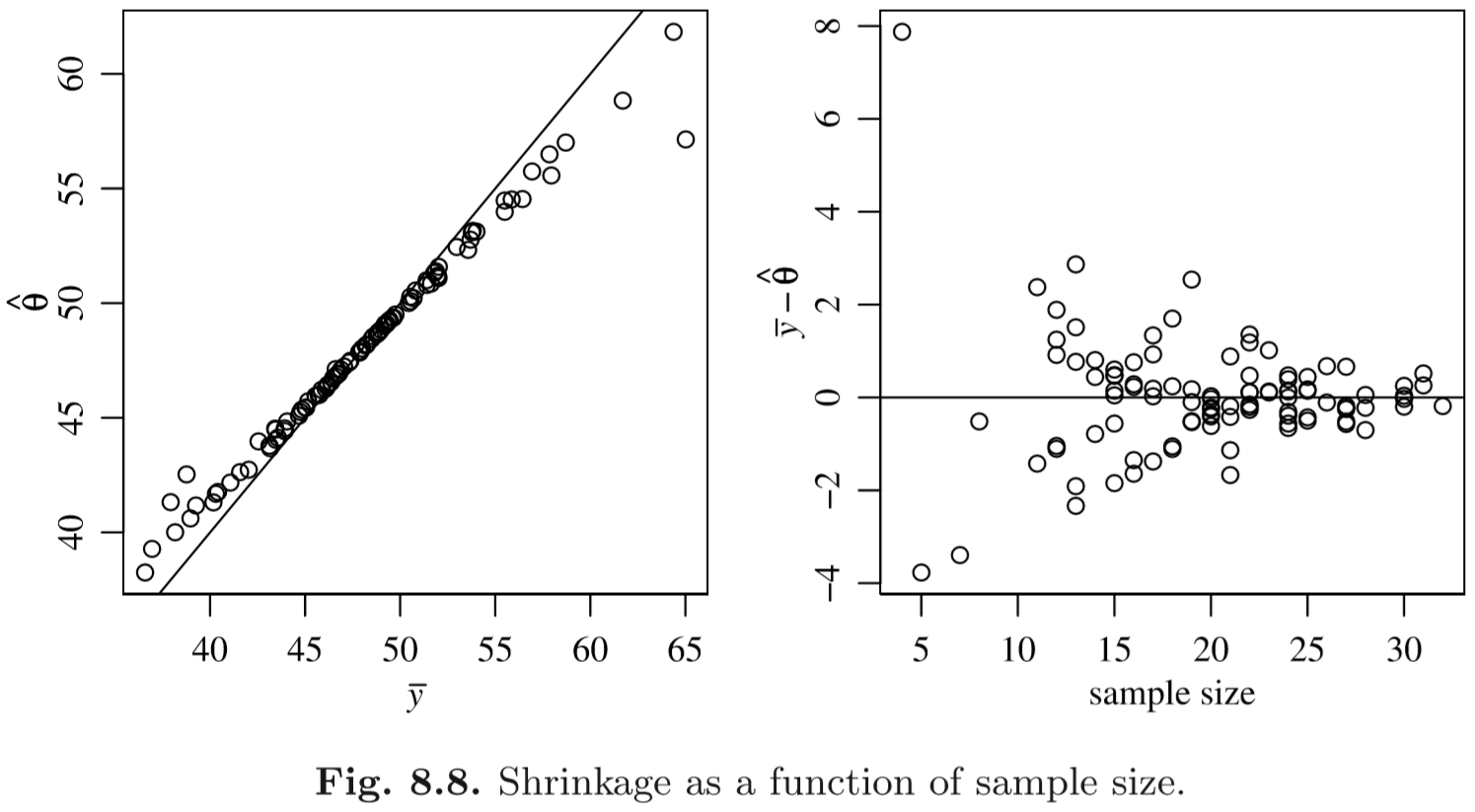
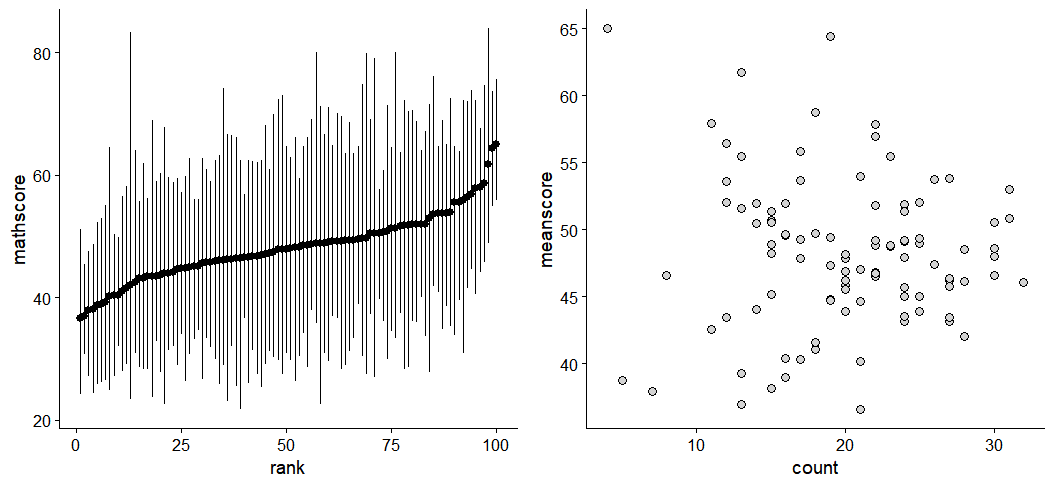
이제 이 식들을 이용해 Gibbs Sampler를 진행하면 된다. 이때 우리가 세운 모델에서는 각 집단의 평균들이 모두 동일한 분포에서 가정하였기 때문에, 표본평균에 비하여 생성된 $\theta_j$의 평균 $E[\theta_j|\mathbf{D}]$은 서로 가까워질 것이다. 즉 표본평균이 높은 그룹은 낮게, 낮은 그룹은 높게 “보정"이 될 것이고, 특히 표본 수가 낮아서 sampling variability가 클수록 이런 보정의 정도가 클 것이다.
무슨 말인지 예를 들어보자. 다음과 같은 데이터가 있다고 하자.
library(dplyr)
Y.school.mathscore = dget('http://www2.stat.duke.edu/~pdh10/FCBS/Inline/Y.school.mathscore')
school.df = Y.school.mathscore %>% as.data.frame %>% as_tibble
meanscore = school.df %>%
group_by(school) %>%
summarise(meanscore = mean(mathscore), count=n()) %>%
mutate(rank=rank(meanscore))
school.toplot = school.df %>%
left_join(meanscore, by='school') %>%
mutate(minscore = min(mathscore), maxscore=max(mathscore))
p1 = ggplot(school.toplot, aes(x=rank, y=mathscore, group=school))+
stat_summary(fun.min =min, fun.max = max, fun=mean)+
theme_cowplot()
p2 = ggplot(meanscore, aes(x=count, y=meanscore))+
geom_point(shape=21, fill = "lightgray", color = "black", size = 3)+
theme_cowplot()
plot_grid(p1, p2)
교재에 나온 코드 대로 깁스 샘플러를 돌려보면 다음과 같이 shrinkage가 발생하며, 특히 표본 수가 작을수록 보정이 더 많이 됨을 알 수 있다.
(Hoff, p.141)
(HW, 필수) Components of variance in hierarchical model
교재 (Hoff, 2009) p.241의 연습문제 8.1 한번 생각해보기. 꼭 제출할 필요는 없음.
(HW, 필수) The eight schools comparison
다음의 사이트를 참조하여
- 베이지안 모델을 이해해서 그림으로 그려보고,
- 이를 시뮬레이션하는 stan 파일을 만들고
- rstan으로 직접 돌려보고 그 결과를 해석하자.
https://www.datascienceblog.net/post/machine-learning/probabilistic_programming/
(Stan 튜토리얼 https://www.mzes.uni-mannheim.de/socialsciencedatalab/article/applied-bayesian-statistics/#validation-and-inference) (Stan이 별로면 그냥 JAGS나 다른거 써도 되고 직접 코드 짜도 된다.)
(HW, 권장) Predicting batting averages (어려움)
다음의 사이트를 참조하여
- 베이지안 모델을 이해해서 그림으로 그려보고,
- 이를 시뮬레이션하는 stan 파일을 만들고
- rstan으로 직접 돌려보고 그 결과를 해석하자.
http://www.probabilaball.com/2016/05/lets-code-mcmc-for-hierarchical-model.html
(HW, 권장) Hierarchical model for economic growth (더 어려움)
다음의 사이트와 첨부한 논문을 참조하여
- 베이지안 모델을 이해해서 그림으로 그려보고,
- 이를 시뮬레이션하는 stan 파일을 만들고
- rstan으로 직접 돌려보고 그 결과를 해석하자.
https://jrnold.github.io/bugs-examples-in-stan/corporatism.html
참고로 이 데이터를 받으려면 다음과 같이 bayesjackman 패키지를 설치해야 한다.
install.packages("devtools")
devtools::install_github("jrnold/jackman-bayes", subdir = "bayesjackman")
data("corporatism", package = "bayesjackman")
이렇게하면 corporatism 데이터가 작업환경에 변수로 저장이 되어있다.
References
- Hoff, P. D. (2009). A first course in Bayesian statistical methods. New York: Springer.
- 그 외 위에 있는 링크들