Note on Kullback-Leibler Divergence

How do we quantify an amount of information that some data $x$ contains? If the data is pretty much expected than it tells nothing new to us. But if it is so rare then it has some value. In this sense, we can think of an amount of information as a “degree of surprise”, and define

$$ \text{information content of data $x$:}\quad h(x) = -\log p(x) $$

where the logarithm ensures $h(x,y)=h(x)+h(y) \Leftrightarrow p(x,y)=p(x)p(y)$, and the negative sign makes $h(x)\geq 0$. Note that if we use $\log_2$ instead, then $h(x)=-\log_2p(x)$ indicates a number of bits to encode an information in $x$. Data that is less likely (small $p(x)$) requires more bits to encode than more common (high $p(x)$) one.

We define an information of a random variable $x$ with a distribution $p(x)$ as the expectation of its information content;

$$ \text{information content of r.v. $x$:}\quad H(x) = E(h(x))= -\sum_xp(x)\log p(x) $$

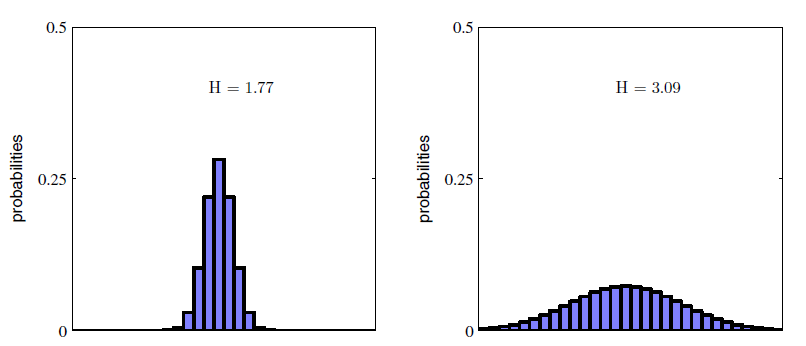
Information of continuous random variable can be defined in a similar way; $H(x)=-\int p(x)\ln p(x)dx$. If one distribution is relatively centered around a region than another, more disperse one, then we would need less coding to do to convey the former distribution as unlikely events (surprises) are less prone to happen.

(source: PRML)

Now suppose we want to convey information of a random variable $x$ with unknown distribution $p(x)$. The information content of $x\sim p(x)$ would be $H(x)=-\int p(x) \ln p(x) dx$. But since we do not know exact form of $p(x)$, we cannot compute $\ln p(x)$ for an observed data $x$. So we might choose another distribution $q(x)$ and approximate $\ln p(x)$ with $\ln q(x)$. Inevitably, by doing so, we shall suffer some degree of information loss $\ln p(x) - \ln q(x)$. Kullback-Leibler divergence is the expected information loss that occurs by approximating $p$ with $q$;

$$ \begin{align} \text{KL divergence:}\quad KL(p|q)&= E_p\Big(\ln\dfrac{p(x)}{q(x)}\Big) \\\
&=\int p(x)(\ln p(x) - \ln q(x))dx \\\
&= -\int p(x)\ln(\dfrac{q(x)}{p(x)})dx \end{align} $$

There are some important properties of KL divergence;

1. KL divergence is NOT a metric. $KL(p|q) \not= KL(q|p)$

2. $KL(p|q)=0$ iff $p(x)=q(x)$

3. $KL(p|q) \geq 0$ ( By Jensen’s inequality, $E(-\ln\dfrac{q(x)}{p(x)}) \geq -\ln E_p(\dfrac{q(x)}{p(x)})=-\ln\int p(x) \dfrac{q(x)}{p(x)} dx=0$ )

References

1. Pattern Recognition and Machine Learning, Bishop, 2006
2. https://bloomberg.github.io/foml/#lectures