(MCMC) 베이지안 사후분포 근사를 위한 MCMC 방법론
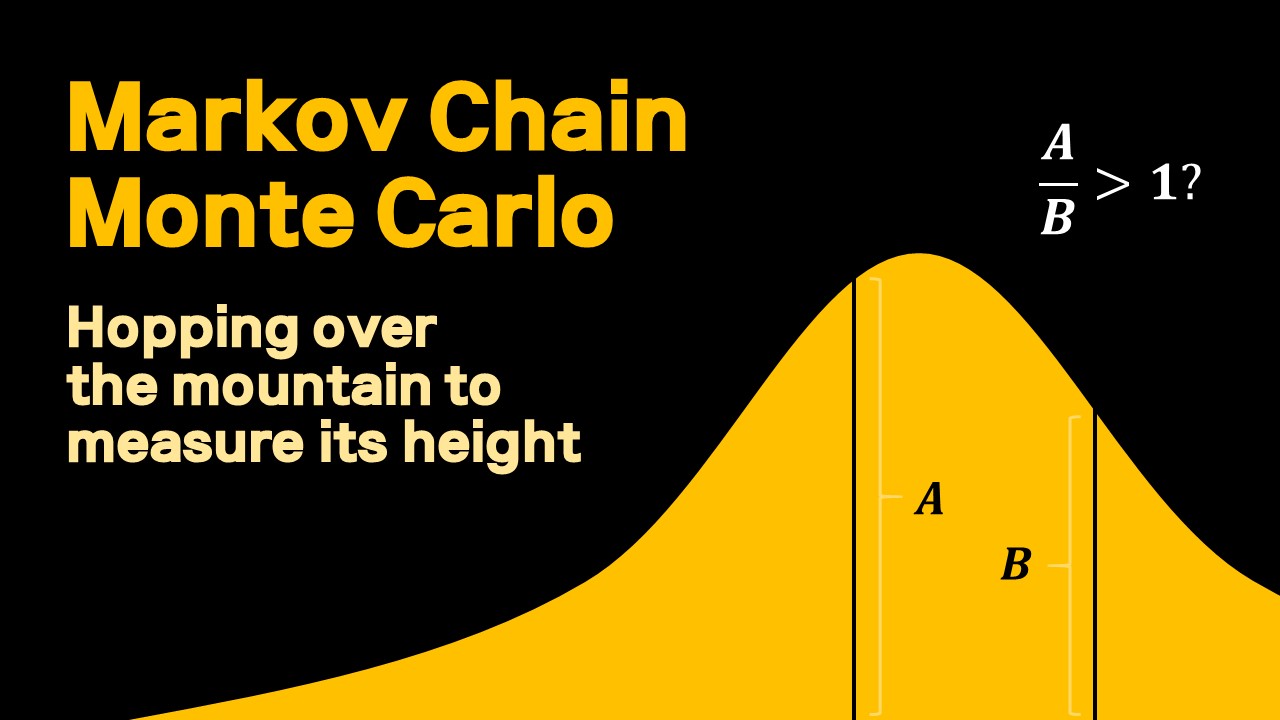
정확한 높이는 몰라도 높고 낮음을 비교할 수는 있다면
0. 개요 베이지안에서 모수에 대한 추론은 곧 모수의 분포를 구하는 것이다. 미지의 수에 대한 불확실성을 확률로 표현하였으니, 베이즈 정리를 이용해 데이터의 불확실성과 거짓말처럼 깔끔하게 같이 섞을 수 있기 때문이다. 그러나 아쉽게도 그 결과로 나오는 분포는 항상 깔끔하지만은 않다. 물론 데이터에 대한 모델을 지수분포족으로 한정하고, 그에 대응하는 또다른 특별한 지수분포족 분포함수를 사용하면, 사후분포의 모수를 쉽게 구할 수 있는데, 이러한 경우를 Prior-Posterior 간에 Conjugacy가 있다고 한다. 그러나 많은 경우 복잡한 데이터에 맞게 모델을 만들다 보면 해석적이지 않은 사후분포에 맞닥뜨리게 된다.
